[BA 3rd Sem Question Papers, Dibrugarh University, 2013, Mathematics, Major, Coordinate Geometry and Algebra - I]
GROUP – A
(Coordinate Geometry)
SECTION – I
(2-Dimension)
(Marks: 27)
1. (a) What will be the equation of the line 
when the origin is transferred to the point 
1
when the origin is transferred to the point 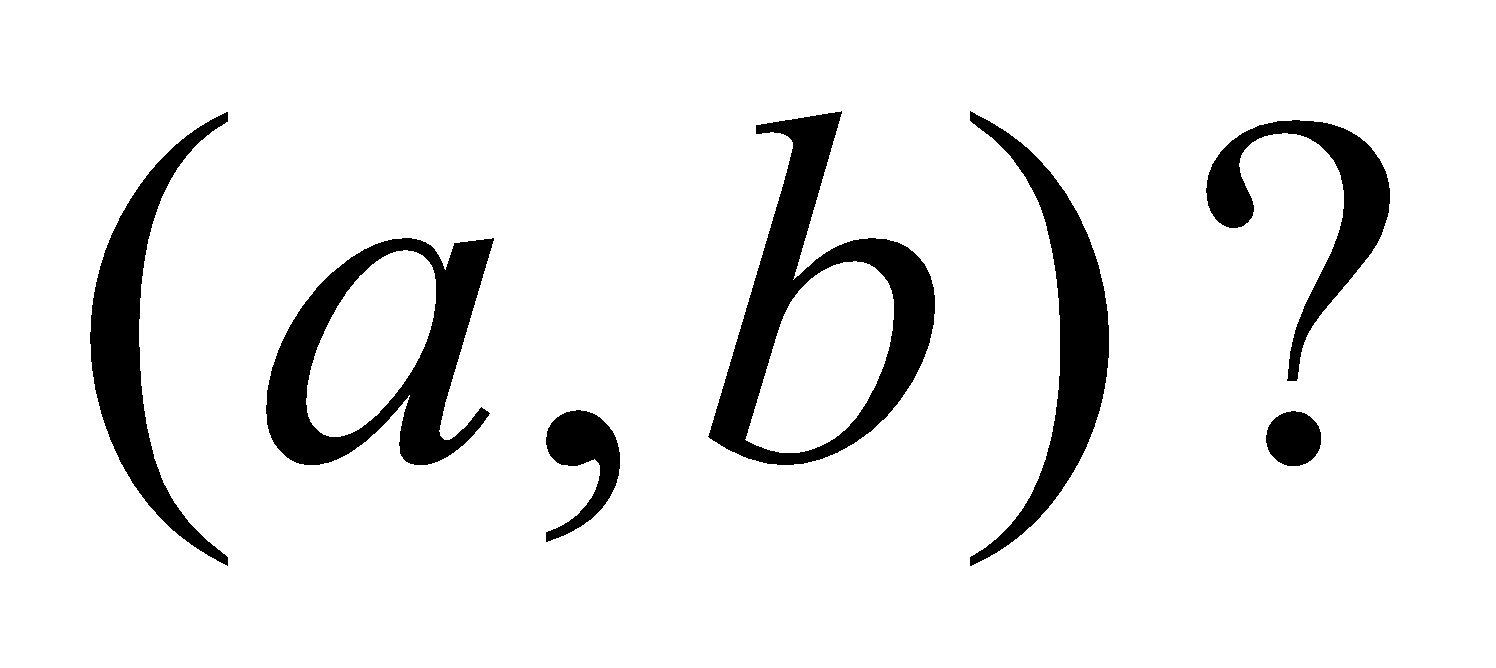1
(b) Transform the equation 
referred to new axes through 
rotated through an angle 
4
referred to new axes through 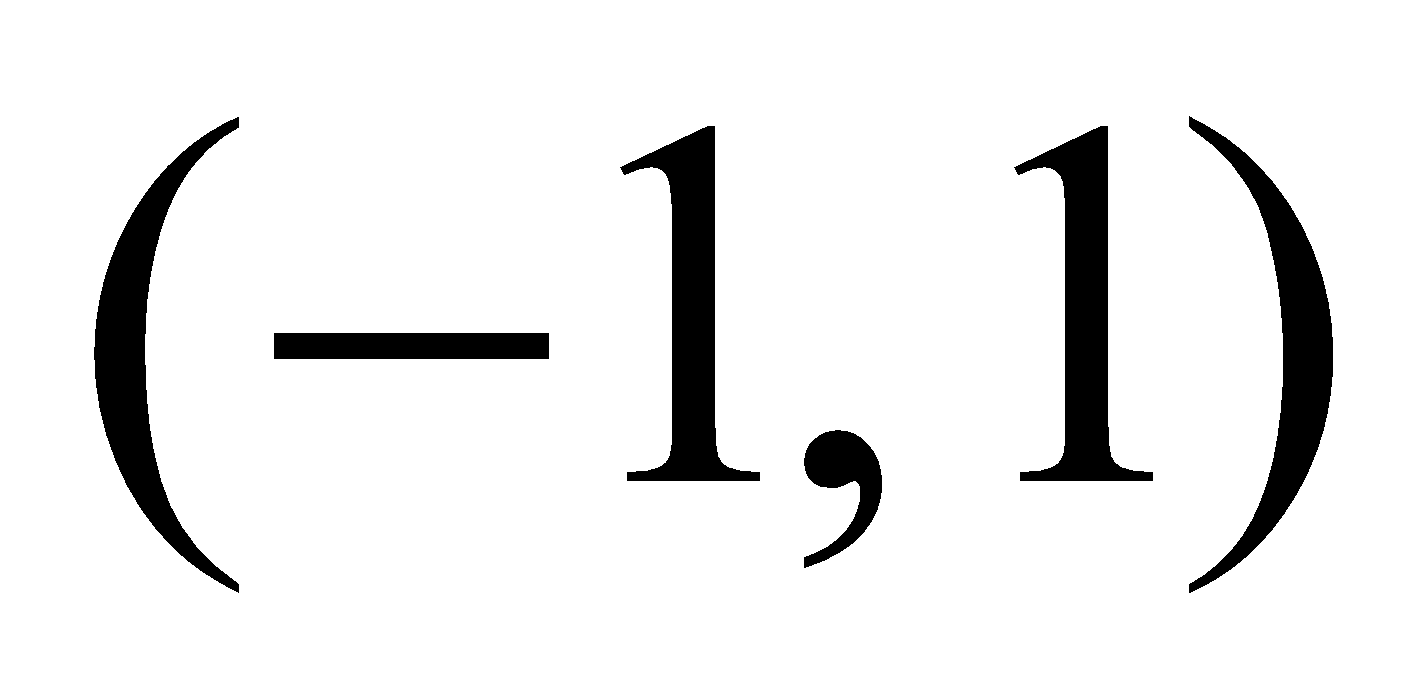rotated through an angle 4
Or
Find the transformed equation of the curve 
when the two perpendicular lines 
and 
are taken as coordinate axes.
when the two perpendicular lines and are taken as coordinate axes.
2. (a) Interpret the situation for the straight lines given by 
when 
1
when 1
(b) Prove that the lines represented by 
have the same pair of bisectors for all values of
. 2
have the same pair of bisectors for all values of. 2
(c) Show that the general equation of 2nd degree
represents a pair of parallel straight lines if 
4
represents a pair of parallel straight lines if 4
Or
Find the condition that one of the lines given by 
may be perpendicular to one of the lines given by
.
may be perpendicular to one of the lines given by.
(d) If 
represents a pair of lines, then prove that the square of the distance of their point of intersection from the origin is 
5
represents a pair of lines, then prove that the square of the distance of their point of intersection from the origin is 5
Or
If 
represents a pair of lines, then prove that the product of the perpendiculars from the origin on these lines is 
represents a pair of lines, then prove that the product of the perpendiculars from the origin on these lines is
3. (a) State True or False: A parabola has its centre at infinity. 1
(b) From the equation of the diameter of the conic 
conjugate to the diameter 
3
conjugate to the diameter 3
(c) Define a conic section. Reduce the equation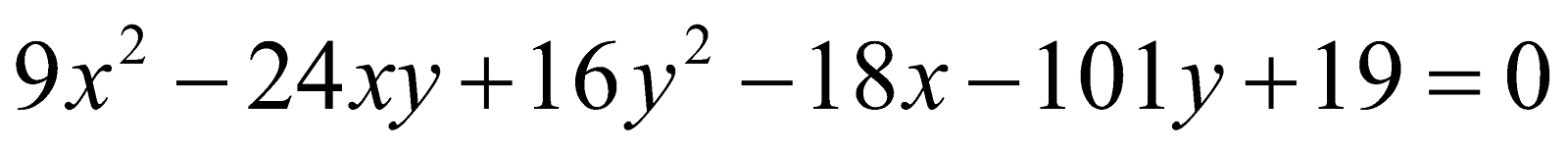
to the standard form. 1+5=6
to the standard form. 1+5=6
Or
Find the equation of the polar of a given point 
with respect to the conic 6 
with respect to the conic 6
SECTION – II
(3-Dimension)
4. (a) State the intercepts made on the axes by the plane 
1
1
(b) Find the equation of the plane through the points 
and 
and parallel to the y-axis. 3
and and parallel to the y-axis. 3
(c) Write the equation of the line through the point 
parallel to the z-plane. 1
parallel to the z-plane. 1
(d) Put the equations 
of a line in the symmetrical form. 5
of a line in the symmetrical form. 5
Or
Find the equation of the plane through the line 
parallel to the line
parallel to the line 
5. (a) Fill up the blank: 1
If the shortest distance between two lines is zero, then the lines are ____.
(b) Find the shortest distance between the y-axis and the line 2
(c) Find the shortest distance between the lines
and
And the equation of the line that represents shortest distance. 5
Or
Find the length and equations of the line of the shortest distance between the lines
and 
GROUP – B
(Algebra – I)
(Marks: 35)
6. (a) State True or False: 1
“A map 
is invertible iff it is one-one into.”
is invertible iff it is one-one into.”
(b) Give an example to show that a coset may not be a subgroup of a group. 1
(c) If 
be a group of prime order 
, then show that has no proper subgroup. 2
be a group of prime order , then show that has no proper subgroup. 2
(d) Answer any two questions: 3x2=6
- Show that an infinite cyclic group has precisely two generators.
- Let H, K be subgroups of G. Show that HK is a subgroup of G if and only if HK = KH.
- Let G be a group. Show that
where n is an integer and
7. Answer any two questions: 5x2=10
- Prove that the set of matrices
where 
is a real number, forms a group under matrix multiplication.
is a real number, forms a group under matrix multiplication. - Show that if G is a group of order 10, then it must have a subgroup of order 5.
- State and prove Lagrange’s theorem.
8. (a) Define normal subgroup. 1
(b) If G is a finite group and N is a normal subgroup of G, then prove that 2
(c) If 
be a homomorphism, then prove that Ker 
is a normal subgroup of 
3
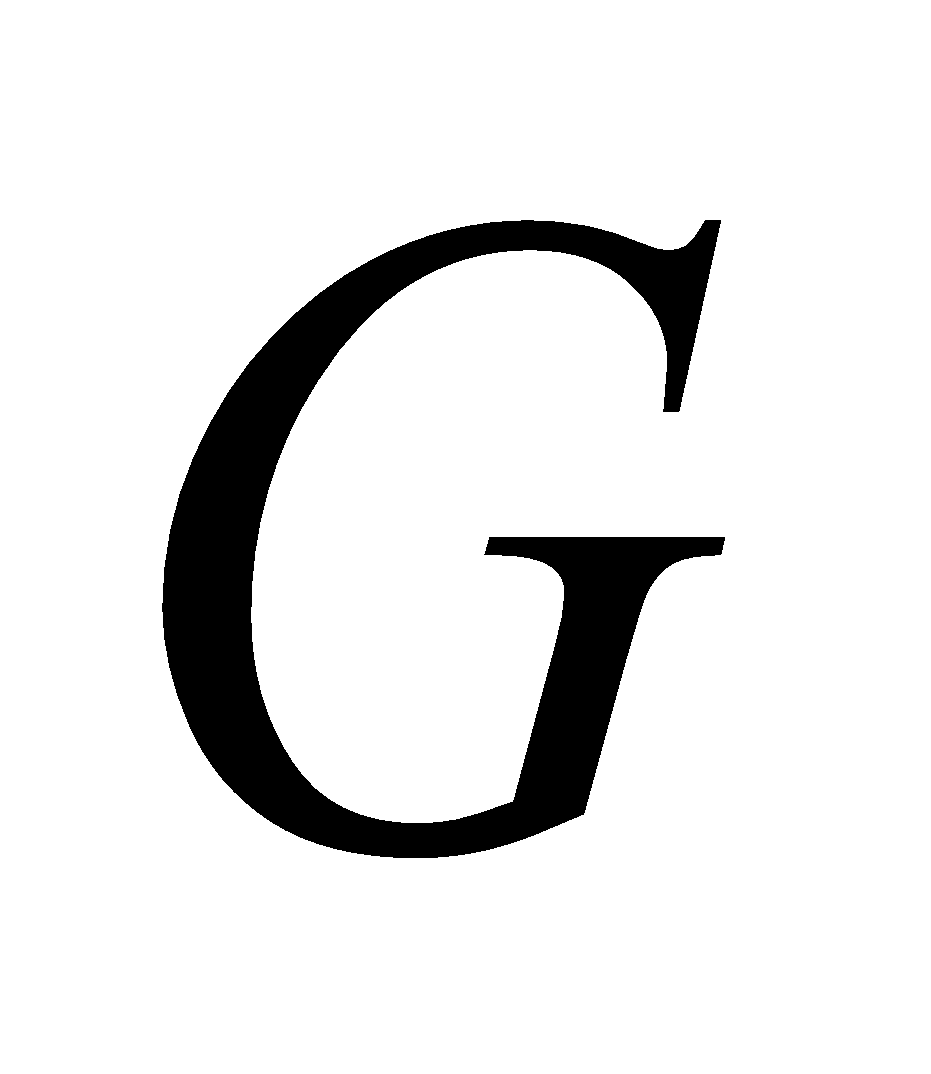be a homomorphism, then prove that Ker is a normal subgroup of 3
9. Answer any one question: 4
(a) If is a homomorphism, then prove that -
is a homomorphism, then prove that -;
an integer where 
and 
are identify elements of 
and 
respectively.
(b) If H and K are two subgroups which are not normal subgroups, then HK is a normal subgroup. Justify with an example.
Also Read: Dibrugarh University Question Papers
10. Answer any one question: 5
- Show that a subgroup H of a group G is normal in G if and only if
- Show that every group is isomorphic to a permutation group.
***
Post a Comment
Kindly give your valuable feedback to improve this website.