[BA 4th Sem Question Papers, Dibrugarh University, 2015, Mathematics, Major, Linear Programming and Analysis - II]
GROUP – A
(Linear Programming)
(Marks: 45)
1. (a) How many components are essential to formulate any LP Problem? 1
(b) Write down the general linear programming problem with 
decision variables and 
constraints. 2
decision variables and constraints. 2
(c) Evening shift resident doctors in a Government hospital work five consecutive days and have two consecutive days-off. Their five days of work can start on any day of the week and the schedule rotates indefinitely. The hospital requires the following minimum number of doctors working:
Sun
|
Mon
|
Tues
|
Wed
|
Thurs
|
Fri
|
Sat
|
35
|
55
|
60
|
50
|
60
|
50
|
45
|
No more than 40 doctors can start their five working days on the same day. Formulate a general linear programming model to minimize the number of doctors employed by the hospital. 3
(d) The graphical method to solve the following LP problem: 4
Maximize
Subject to the constraints
And 
2. (a) What type of variables needed to add in the given LP Problem to convert it into standard form when the constraints is ‘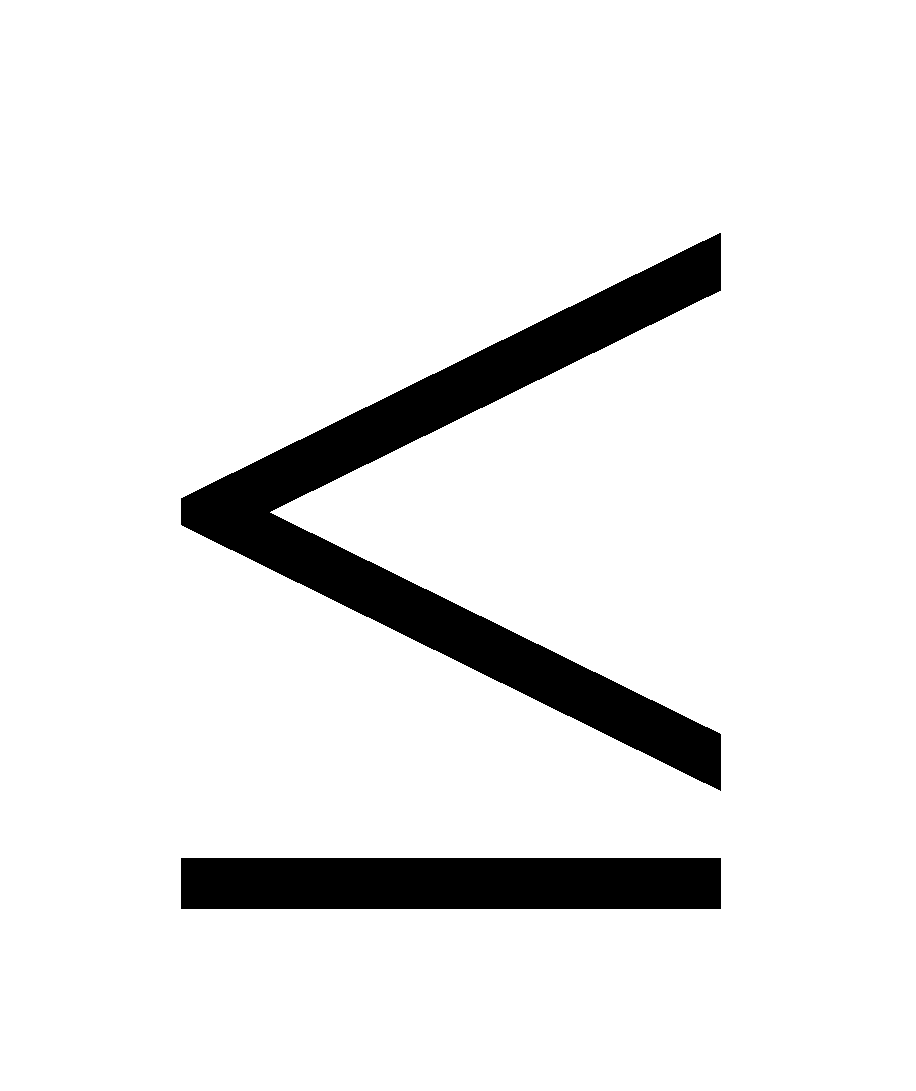
’ type? 1
’ type? 1
(b) Write down the key column from the following table: 2
 |  |  |  |  |  |  |  | |
0
|  |
8
|
2
|
3
|
0
|
1
|
0
|
0
|
0
|  |
10
|
0
|
2
|
5
|
0
|
1
|
0
|
0
|  |
15
|
3
|
2
|
4
|
0
|
0
|
1
|
 |   |
3
|
5
|
4
|
0
|
0
|
0
|
(c) Solve by simplex method: 5
Maximize 
Subject to the constraints
And 
(d) Solve by two-phase method: 7
Minimize
Subject to constraints
And 
Or
Solve by Big-M method:
Maximize
Subject to the constraints
And 
3. (a) State fundamental duality theorem. 1
(b) What should be the type of solution of a dual problem who’s primal has an unbounded solution? 1
(c) Write down the two rules for constructing the dual problem from primal. 2
(d) Find the dual of the following LP problem: 4
Maximize
Subject to the constraints
And 
Or
“If the k-th constraint of a primal be an equation, then the k-th dual variable will be unrestricted in sing.” Prove it.
4. (a) Fill in the blank:
In a balanced transportation problem having 
origins and 
destinations
, the exact number of basic variables is ____. 1
origins and destinations, the exact number of basic variables is ____. 1
(b) Write down the two properties of a loop in a transportation problem. 2
(c) Obtain the initial basic feasible solution to the following transportation problem by Vogel’s approximation method and prove that the solution is degenerate: 9
 |  |  |  |  | |
 |
4
|
6
|
5
|
2
|
6
|
 |
6
|
4
|
1
|
4
|
10
|
 |
5
|
2
|
3
|
1
|
12
|
 |
4
|
6
|
7
|
8
|
14
|
 |
9
|
16
|
10
|
7
|
42
|
Or
Discuss the ‘MODI’ method to test the optimality of a solution to a transportation problem. 9
GROUP – B
[Analysis – Ii (Multiple Integral)]
(Marks: 35)
5. (a) Fill in the blank: 1
The integral of a periodic function over any interval whose length is equal to its period always has the ____.
(b) The function 
is periodic with period 
on the interval
. Find its Fourier series. 4
is periodic with period on the interval. Find its Fourier series. 4
(c) Find the Fourier series of the periodic function 
with period
, defined as 5
with period, defined as 5
Also find the sum of series at 
and 
and
Or
Expand the function
in the interval 
as a sine series.
as a sine series.
6. (a) Define a plane curve. 1
(b) Evaluate the integral 
where 
is the curve 
2
where is the curve 2
(c) Prove that every continuous function in 
is integrable. 4
is integrable. 4
(d) State and prove Green’s theorem. 1+5=6
Or
Change the order of integration
and also prove that 
where 
where
6
Also Read: Dibrugarh University Question Papers
7. (a) State Gauss’ theorem. 1
(b) Express a surface integral in terms of a double integral. 2
(c) Find the volume of the sphere 
using polar coordinates. 3
using polar coordinates. 3
(d) Prove Stokes theorem. 6
Or
Compute the volume of the ellipsoid
***
Post a Comment
Kindly give your valuable feedback to improve this website.