[BA 2nd Sem Question Papers, Dibrugarh University, 2016, Mathematics, General, Matrices, Ordinary Differential Equations and Numerical Analysis]
2016 (Nov)
MATHEMATICS (General)
Course: 201
(Matrices, Ordinary Differential Equations and Numerical Analysis)
Full Marks: 80
Pass Marks: 32 / 24
Time: 3 hours
The figures in the margin indicate full marks for the questions
GROUP – A
(Matrices)
(Marks: 20)
1. (a) Define rank of a matrix. 1
(b) Find the rank of the following matrix by reducing it to normal form: 4
(c) Show that – 3
rank
2. (a) Show that the following equations are consistent and find their solution: 5
(b) Define characteristic roots and characteristic vectors. 2
(c) State and prove Cayley-Hamilton theorem. 5
Or
Determine the characteristic roots and corresponding characteristic vectors of the following matrix: 5
GROUP – B
(Ordinary Differential Equations)
(Marks: 30)
3. (a) Write the standard form of second-order linear differential equation. 1
(b) Solve any one: 3
(c) Solve any one: 3
, where
(d) Using the transformation , reduce the following equation to a linear differential equation: 3
, reduce the following equation to a linear differential equation: 3
4. (a) Solve any two: 3x2=6
(b) Solve any one: 4
5. Answer any two questions: 5x2=10
- Removing the first-order derivative, solve the following equation:
- Solve by changing the independent variable:
- Apply the method of variation of parameter to solve the equation
where 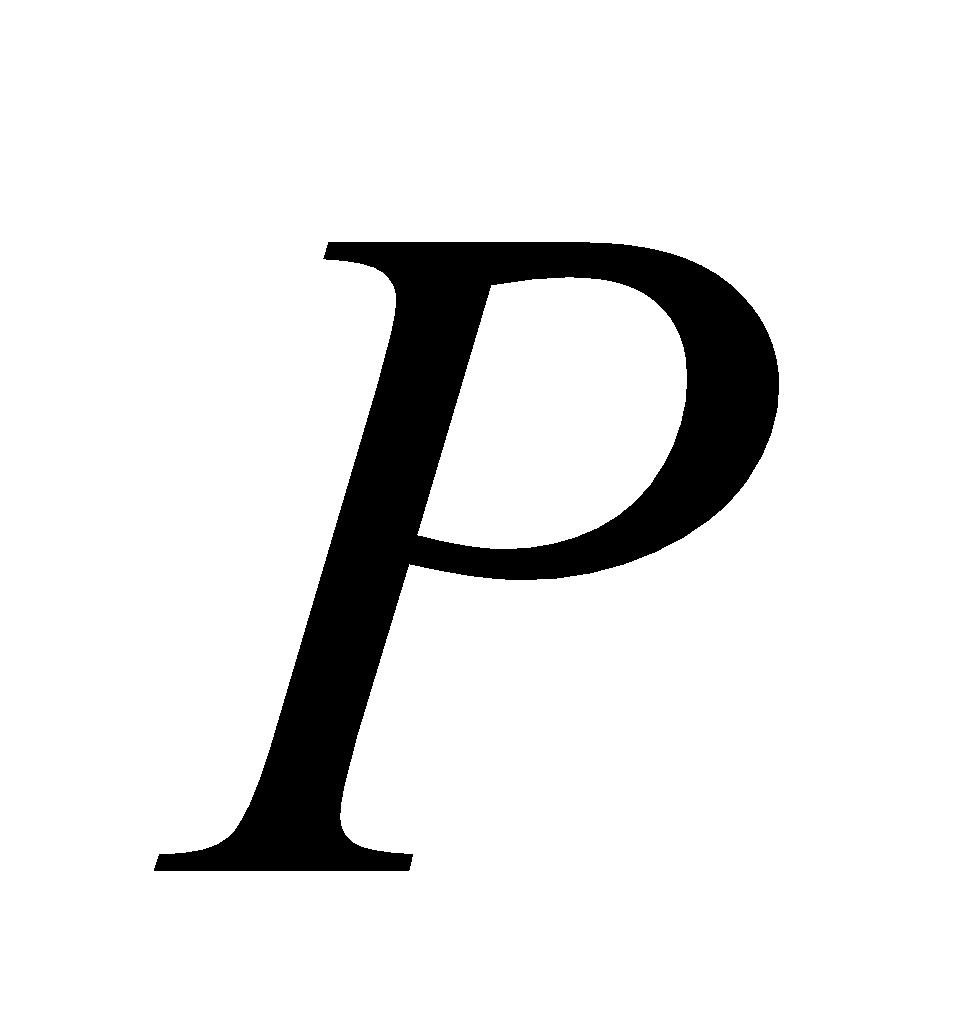 ,
, and
and  are the functions of
are the functions of  .
.
GROUP – C
(Numerical Analysis)
(Marks: 30)
6. (a) Write True or False: 1
“Bisection method is always convergent”.
(b) Describe Newton-Raphson method for solving an algebraic equation. 4
Or
Find one root of the equation  by using iteration method. 4
by using iteration method. 4
(c) Use of Regula Falsi method to obtain a root of  correct to three decimal places 4
correct to three decimal places 4
Or
Find the real root of the equation  using bisection method. 4
using bisection method. 4
(d) Solve by Gauss-Jordan method: 6
Or
Describe Gauss elimination method to solve the system of linear equations. 6
7. (a) Define operator  . 1
. 1
(b) Evaluate: 2
(c) Show that – 2
(d) Deduce Lagrange’s interpolation formula. 5
Or
Given –
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
| |
1
|
8
|
27
|
64
|
125
|
216
|
434
|
512
|
Then find 
Also Read: Dibrugarh University Question Papers
(e) Derive Simpson’s one-third rule for numerical integration. 5
Or
Find
by trapezoidal rule.
***


Post a Comment
Kindly give your valuable feedback to improve this website.