[BA 2nd Sem Question Papers, Dibrugarh University, 2015, Mathematics, General, Matrices, Ordinary Differential Equaitons and Numerical Analysis]
2015 (May)
MATIEMATICS (General)
Course: 201
(Matrices, Ordinary Differential Equations and Numerical Analysis)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
GROUP – A
(Matrices)
(Marks: 20)
1. (a) Define nullity of a matrix. 1
(b) Prove that the rank of transpose of a matrix is same as that of the original matrix. 3
(c) Find the rank of the following matrix by reducing it to echelon form: 4
2. (a) Show that the following equations are consistent and find their solutions: 5
Or
Solve:
(b) Find the characteristic polynomial of the following square matrix: 2
(c) Show that every square matrix satisfies its own characteristic equation. 5
Or
Determine the characteristic roots and corresponding characteristic vectors of the following matrix: 2+3=5
GROUP – B
(Ordinary Differential Equations)
(Marks: 30)
3. (a) Write the necessary condition for the equation
to be an exact differential equation. 1
to be an exact differential equation. 1
(b) Write the integrating factor of the equation
1
1
(c) Define Wronskian of 
functions. 2
functions. 2
(d) Solve any one:
(e) Solve any one:
4. (a) Solve any two: 3x2=6
Given, 
(b) Solve any one: 4
5. Answer either [(a) and (b)] or (c):
(a) If the equation
reduces to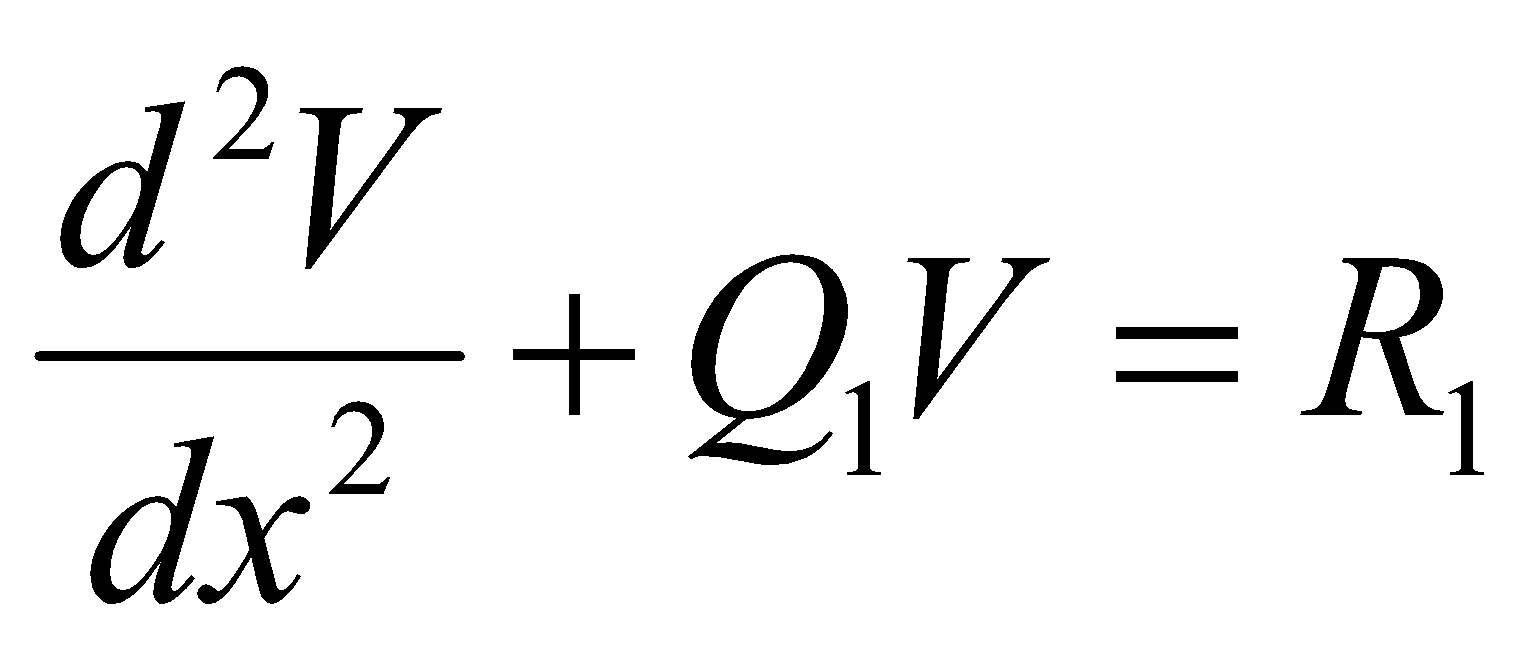
by removing the first-order derivative, then write the value of 
1
by removing the first-order derivative, then write the value of 1
(b) Removing the first-order derivative, solve the following equation: 4
(c) Apply the method of variation of parameter to solve the following equation: 5
6. Transform the equation 5
By changing the independent variable; where
,
andare the functions of 
.
,andare the functions of .
Or
If
is a particular solution of
find its general solution.
is a particular solution offind its general solution.
GROUP – C
(Numerical Analysis)
(Marks: 30)
7. (a) Write True or False: 1
In solving an equation by Newton-Raphson method, the derivative of the function should not be zero.
(b) Find a real root of the following equation by bisection method correct to two places of decimal: 5
Or
Describe iteration method for solving an algebraic equation.
(c) Obtain a formula to compute the square root of a number using Newton-Raphson method. 3
(d) Solve by Gauss elimination method: 6
Or
Describe the solution of system of linear equations by Gauss-Seidel method.
8. (a) Define interpolation. 1
(b) With usual notations, show that 
2
2
(c) Deduce Newton’s backward interpolation formula. 5
Or
Given:
Find
, by using any method of interpolation.
, by using any method of interpolation. Also Read: Dibrugarh University Question Papers
9. (a) Find the general quadrature formula for equidistant ordinates and deduce the trapezoidal rule. 3+2=5
Or
Find the value of 
by Simpson’s.
by Simpson’s.
(b) Find
by using Lagrange’s interpolation formula from the following table: 2
by using Lagrange’s interpolation formula from the following table: 2 : |
0
|
1
|
2
|
5
|
| : |
2
|
3
|
12
|
147
|
***
Post a Comment
Kindly give your valuable feedback to improve this website.