[BA 2nd Sem Question Papers, Dibrugarh University, 2015, Mathematics, Major, Matrices, Ordinary Differential Equations, Numerical Analysis]
2015 (May)
MATHEMATICS (Major)
Course: 201
(Matrices, Ordinary Differential Equations, Numerical Analysis)
Full Marks: 80
Pass Marks: 32/24
Time: 3 hours
The figures in the margin indicate full marks for the questions
A: Matrices
(Marks: 20)
1. (a) Under what condition, the rank of the following matrix is
is  ? 1
? 1
(b) Show that the rank of a skew-symmetric matrix cannot be one. 2
(c) Reduce the matrix to its normal form and hence find its rank: 5
to its normal form and hence find its rank: 5
Or
Find non-singular matrices and
and such that
such that is in the normal form where
is in the normal form where
2. (a) Under what condition, a system of homogeneous linear equations
homogeneous linear equations in
in unknowns has only trivial solution? 1
unknowns has only trivial solution? 1
(b) What is the eigenvalues of , if eigenvalues of matrix
, if eigenvalues of matrix is
is . 1
. 1
(c) Investigate for what values of and
and , the simultaneous equations.
, the simultaneous equations.
Have (i) no solution, (ii) a unique solution and (iii) an infinite number of solutions. 4
(d) State and prove Cayley-Hamilton theorem. 6
Or
Find the characteristic roots and associated characteristic vectors for the matrix.
B: Ordinary Differential Equation
(Marks: 30)
3. (a) Is the differential equation exact? 1
exact? 1
(b) Find the integrating factor of the differential equation 2
2
(c) Solve (any one): 3
(d) If and
and are any two solutions of
are any two solutions of , then prove that the linear combination
, then prove that the linear combination , where
, where and
and  are constants, is also a solution of the given equation. 4
are constants, is also a solution of the given equation. 4
Or
Show that linearly independent solutions of are
are
 and
and
 . What is the general solution? Find the solution
. What is the general solution? Find the solution with the property
with the property .
.
4. (a) If auxiliary equations has tow equal pairs of imaginary roots, then what is the general solution of the second-order linear differential equation? 1
(b) What is the value of  if?
if?  1
1
(c) Solve (any two): 4x2=8
(d) Solve (any two): 5x2=10
(by removing first-order derivative)
(by changing the independent variable)
(by applying the method of variation of parameters)
C: Numerical Analysis
(Marks: 30)
5. (a) Fill in the blank: 1
If is continuous in the interval
is continuous in the interval and if
and if and
and are of opposite signs then the equation
are of opposite signs then the equation  will have ____ real root between
will have ____ real root between and
and . 1
. 1
(b) What is the length of the subinterval which contains  after
after  bisections?
bisections?
(c) Using regula falsi method, find the first approximate value of the root of the equation  that lies between 2.5 and 3. 3
that lies between 2.5 and 3. 3
(d) Answer (any two): 5x2=10
- Describe Newton-Raphson method for obtaining the real roots of the equation
.
- Apply Gauss-Jordan method, to find the solution of the following system:
- Solve by Gauss-Seidel method
Also Read: Dibrugarh University Question Papers
6. (a) State Trapezoidal rule. 1
(b) Show that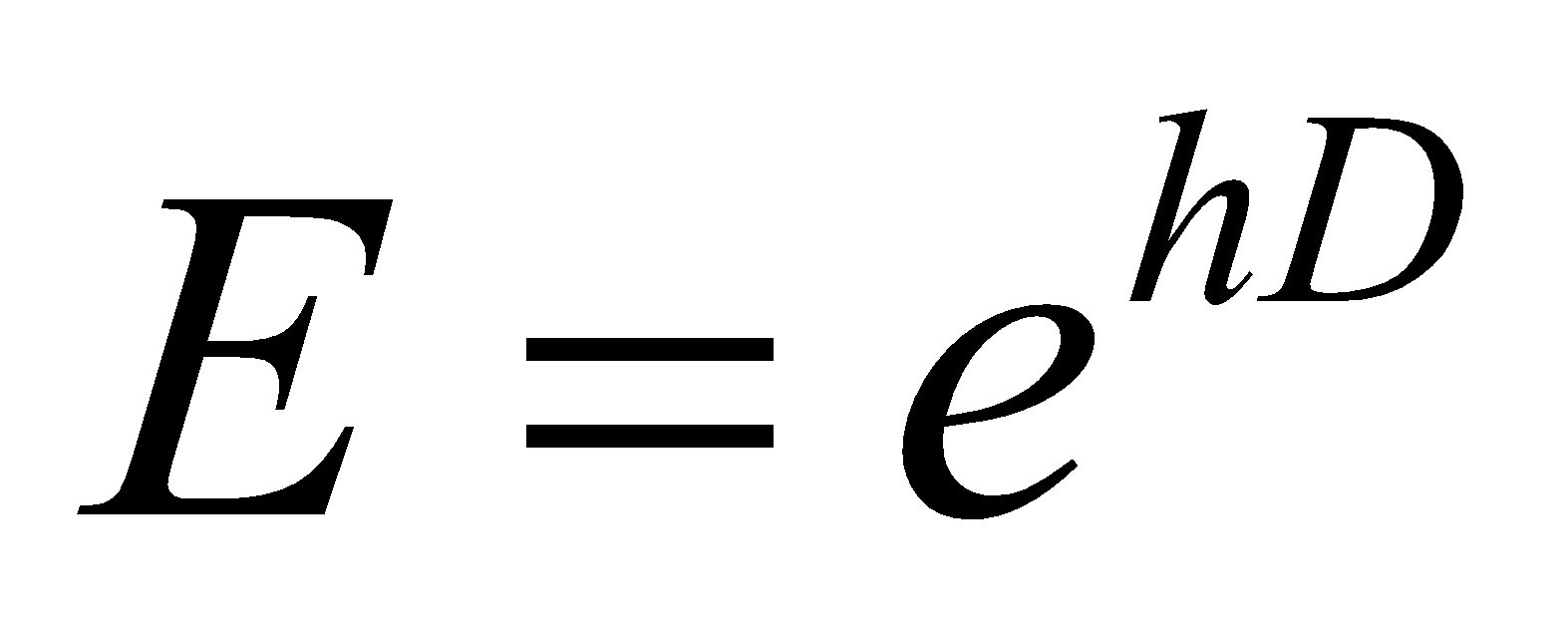 , where the symbols have their usual meanings. 2
, where the symbols have their usual meanings. 2
(c) Evaluate  2
2
(d) Answer (any two): 5x2=10
- Deduce the Simpson’s one-third rule.
- The population of a town is as follows:
Year (x):
|
1941
|
1951
|
1961
|
1971
|
1981
|
1991
|
Population (in lakhs)(y):
|
20
|
24
|
29
|
36
|
46
|
51
|
Estimate the population increase during the period 1946 to 1976.
- Evaluate
by trapezoidal rule.
***


Post a Comment
Kindly give your valuable feedback to improve this website.