[BA 2nd Sem Question Papers, Dibrugarh University, 2016, Mathematics, Majro, Matrices, Ordinary Differential Equations, Numerical Analysis]
2016 (May)
MATHEMATICS (Major)
Course: 201
(Matrices, Ordinary Differential Equations, Numerical Analysis)
Full Marks: 80
Pass Marks: 32/24
Time: 3 hours
The figures in the margin indicate full marks for the questions
1. (a) State whether True or False: 1
Rank of a matrix is a positive integer.
(b) Define elementary transformations of matrices. 2
(c) Show that rank of the product of two matrices cannot exceed that of either matrix. 5
2. (a) Show that the following equations are consistent and solve them by matrix method: 6
Or
State and prove Cayley-Hamilton theorem. 6
(b) Find the characteristic values and characteristic vectors of the following matrix: 6
B: Ordinary Differential Equations
(Marks: 30)
3. (a) Find the integrating factor of the differential equation.
and
are functions of
. 1
(b) Solve (any two): 3x2=6
(c) Show that the solutions 
and 
of
and of 
are linearly independent. 3
4. (a) Solve: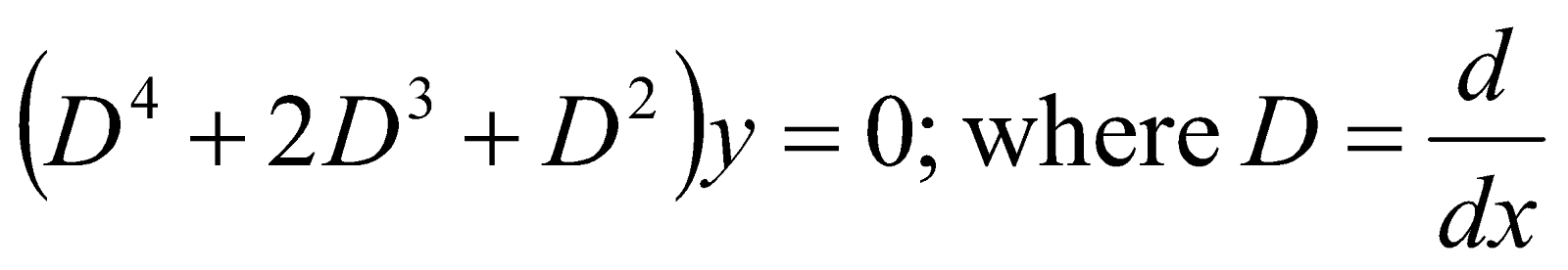 
2
2
(b) Solve (any two): 4x2=8
5. (a) Describe the method of removal of the first derivative of the differential equation
5
(b) Solve (any one): 5
by putting
C: Numerical Analysis
(Marks: 30)
6. (a) Write the condition of convergence of iteration method. 1
(b) In solving system of linear algebraic equation, what are the differences between ‘Gauss elimination method’ and ‘Jordan Method’? 2
(c) Find a real root of the equation
by using bisection method correct to three decimal places. 6
by using bisection method correct to three decimal places. 6
Or
Find a root of the equation
by using Newton Raphson method correct to three decimal places. 6
by using Newton Raphson method correct to three decimal places. 6
(d) Solve the following equations by Gauss-Jordan Method: 6
Also Read: Dibrugarh University Question Papers
7. (a) Define interpolation. 1
(b) Evaluate
2
2
(c) Answer (any two): 6x2=12
- Deduce ‘Newton’s forward interpolation formula’.
- Derive Simpson’s one-third rule for numerical integration.
- Evaluate:
By Simpson’s
rule
rule
***
Post a Comment
Kindly give your valuable feedback to improve this website.