Dibrugarh University Arts Question Papers: MATHEMATICS A: (Linear Programming) ' (November) - 2016

byKumar Nirmal Prasad - 0

[BA 4th Sem Question Papers, Dibrugarh University, 2016, Mathematics, General, A: Linear Programming]

2016 (Nov)
MATHEMATICS (General)
Course: 401
(A: (Linear Programming))
Full Marks: 80
Pass Marks: 20/15
Time: 2 ½ hours
The figures in the margin indicate full marks for the questions


1. (a) Give an example of convex set. 1
(b) Write two limitations of LP model. 2
(c) Answer any one question: 4
  1. Prove that the set of all feasible solutions to an , is closed convex set.
  2. A manufacturer produces two types of models and. Each model requires 4 hours of grinding and 2 hours of polishing; whereas each model requires 2 hours of grinding and 5 hours of polishing. The manufacturer has 2 grinders and 3 polishers. Each grinder works for 40 hours a week and each polisher works for 60 hours a week. Profit on an model is Rs. 3 and on an model is Rs. 4. Whatever is produced in a week is sold in the market. How should the manufacturer allocate his production capacity to the two types of models so that he may make the maximum profit in a week?
(d) Solve graphically any one of the following:
  1. Maximize
Subject to
And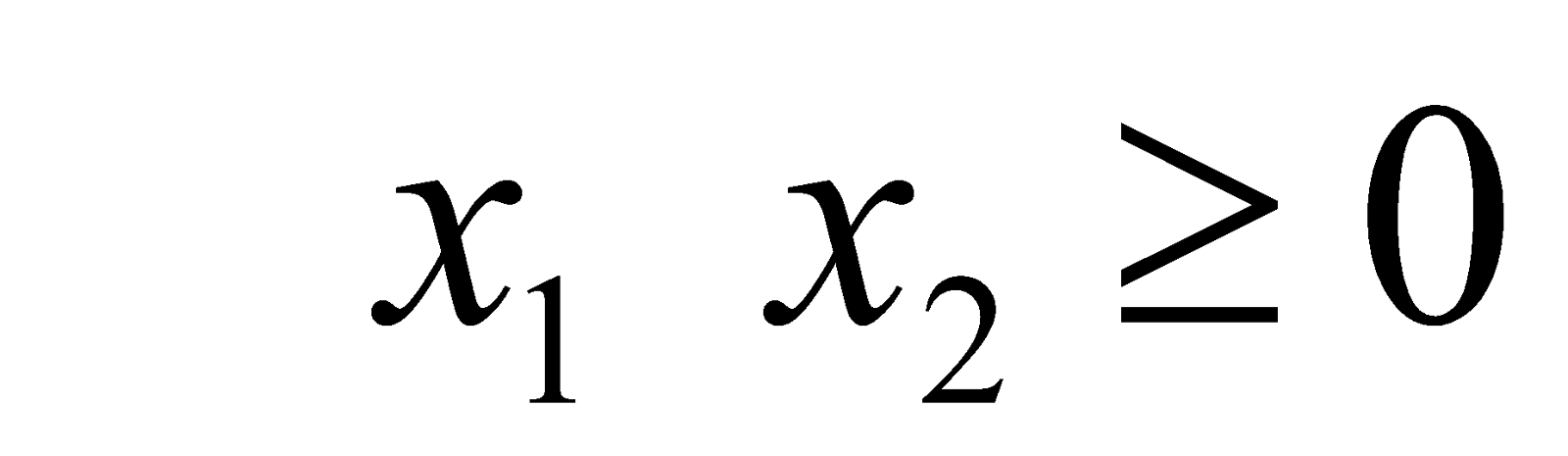
  1. Minimize
Subject to
And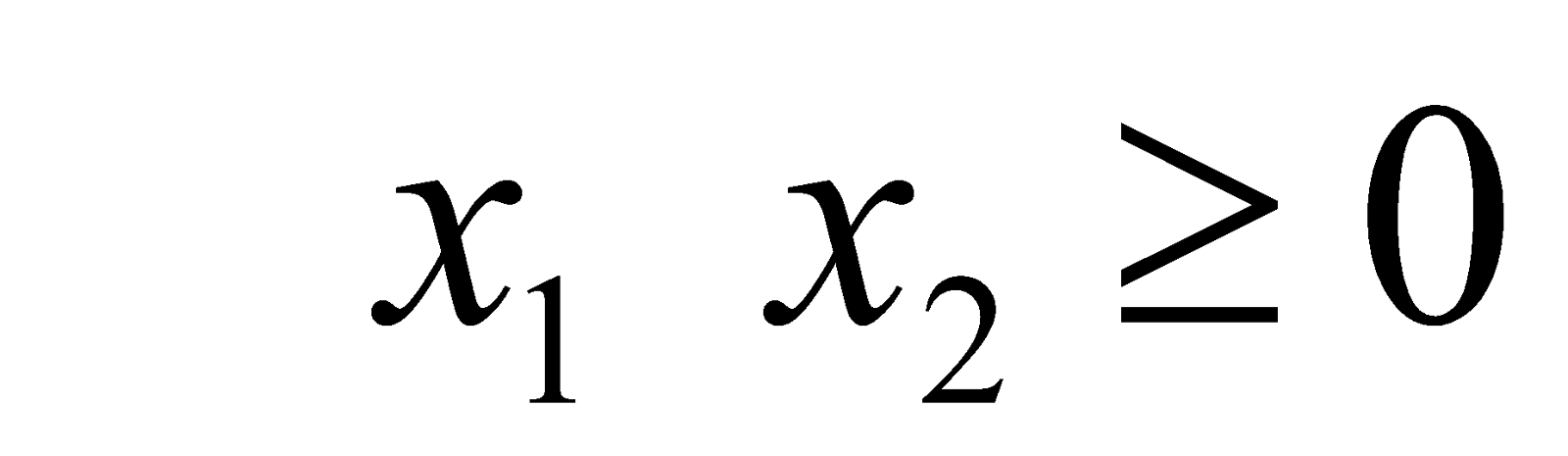
2. (a) Who developed the solution of LPP using simplex method? 1
(b) Mention the difference between ‘feasible solution’ and ‘basic feasible solution’ in an LPP. 2
(c) Using simplex method, solve any one of the following LPP: 7
  1. Maximize
Subject to
And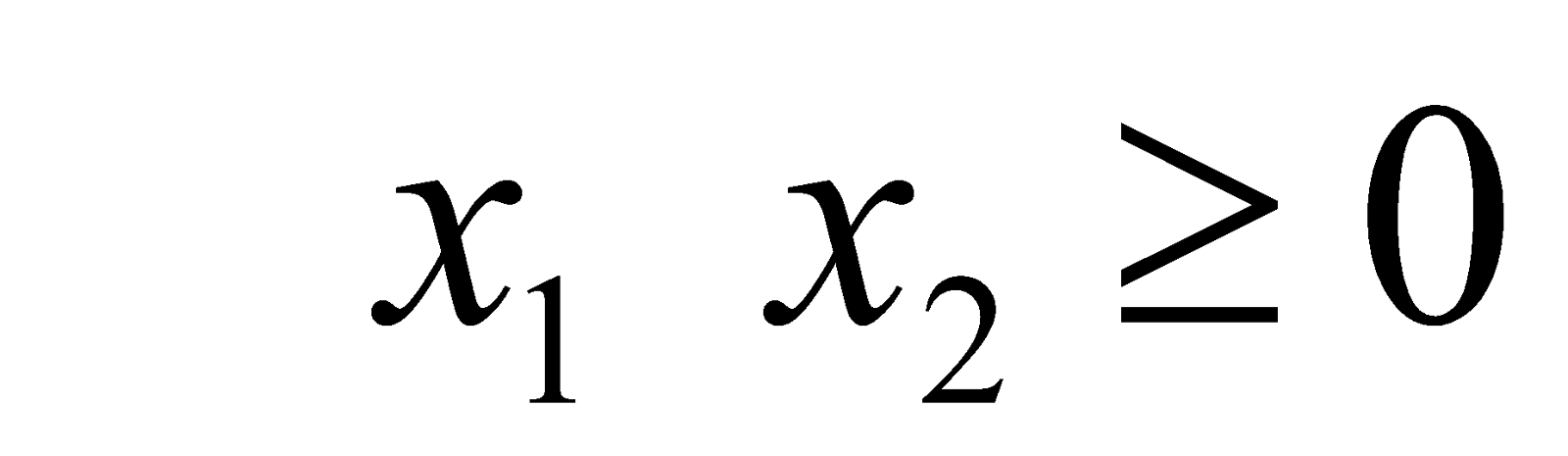
  1. Minimize
Subject to
And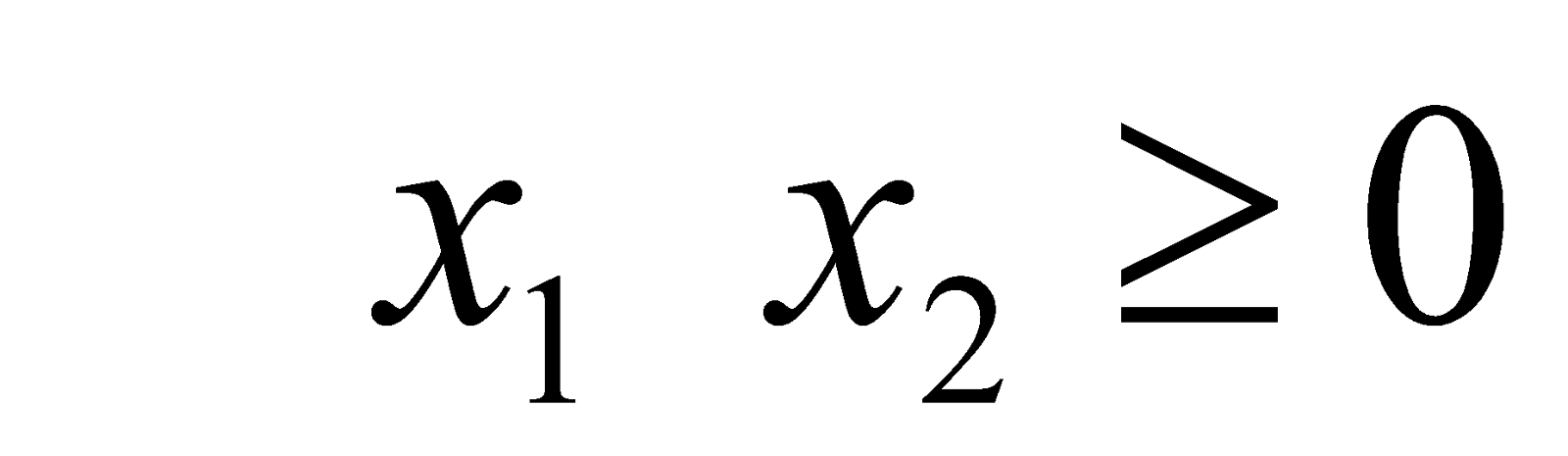
(d) Answer either (i) or (ii):
  1. Solve the following using two-phase method:
Minimize
Subject to
and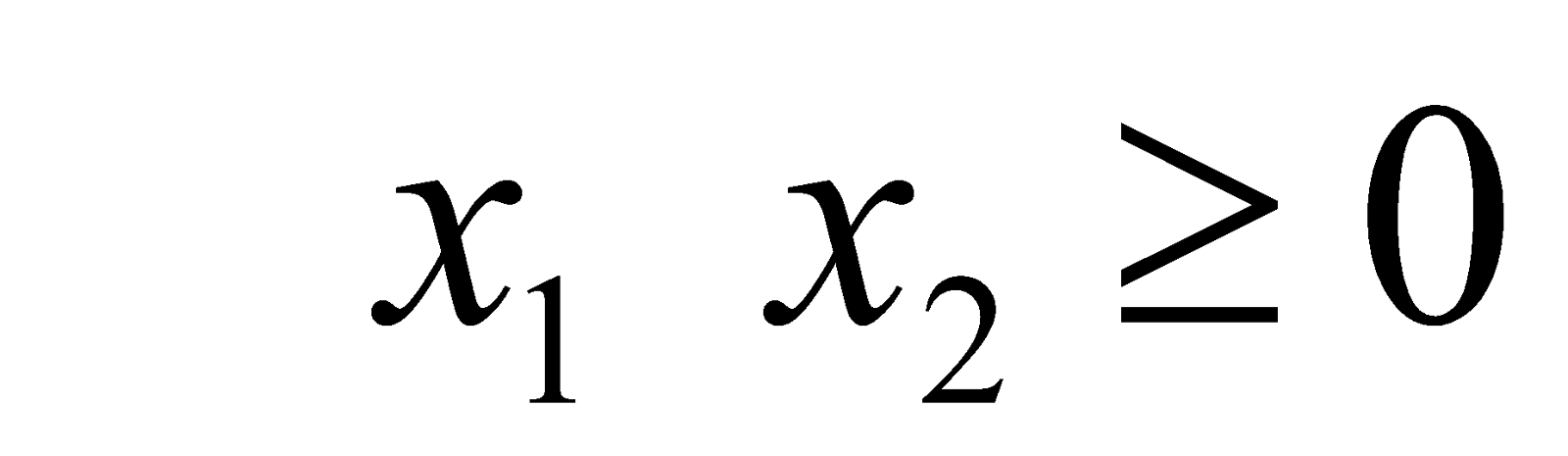
  1. Using Big-M method, solve the following :
Minimize
Subject to
and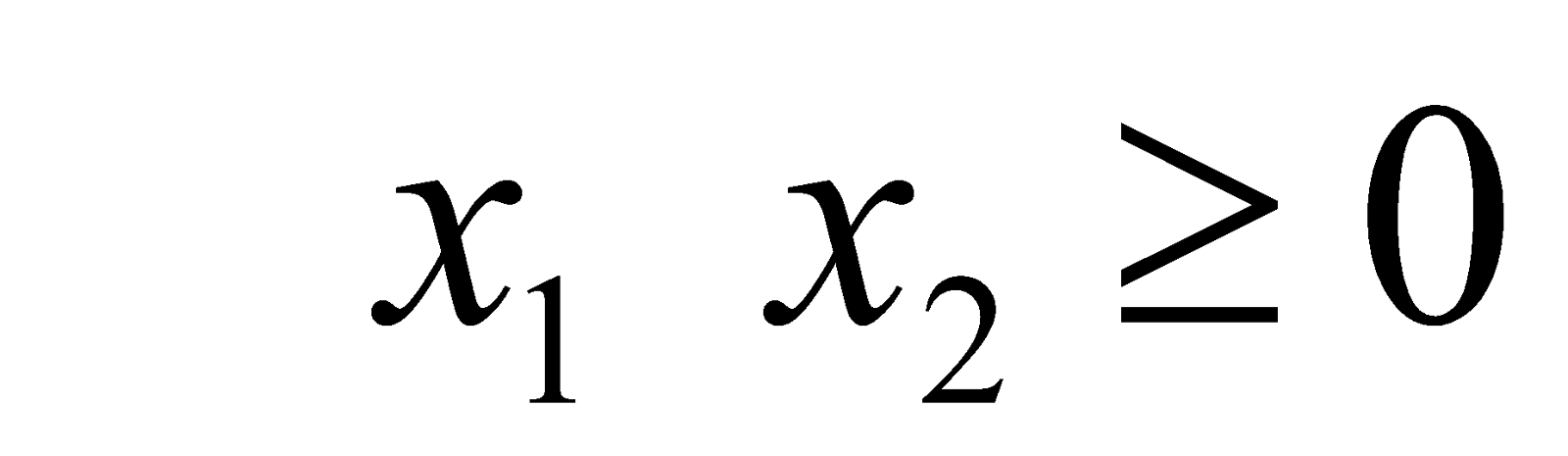
3. (a) If the variable in primal is unrestricted in sign, then what about the dual constraint? 1
(b) Write two advantages of duality. 2
(c) Answer any one question: 5
  1. Obtain the dual problem of the following primal LP problem:
Minimize
Subject to
And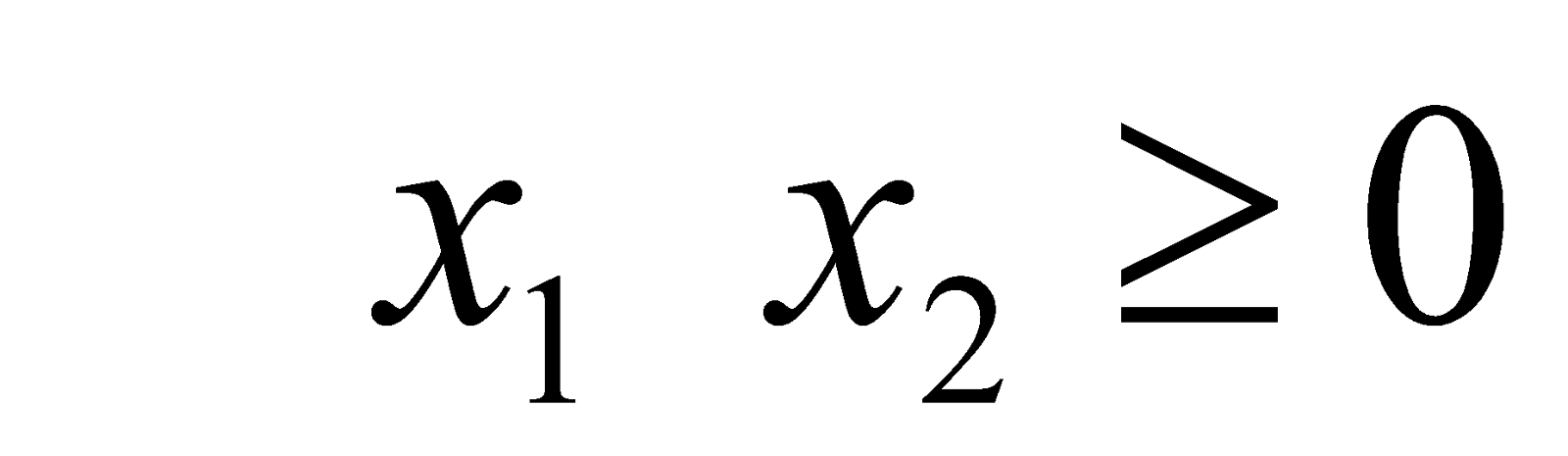
  1. Prove that if the primal problem has an unbounded solution, then the dual problem has either no solution or an unbounded solution.
4. (a) Answer the following questions: 1x2=2
  1. What do you mean by a balanced transportation problem?
  2. Define loop of a transportation table.
(b) Write the mathematical formulation of transportation problem. 2
5. Answer any one question: 8
  1. Solve the following transportation problem using ‘least cost method’:

Supply
1
2
1
4
30
3
3
2
1
50
4
2
5
9
20
Demand
20
40
30
10
100
  1. Write a short note on Vogel’s approximation. 4
  2. Prove that there exists a feasible solution in each transportation problem, which is given by

***
Tags

Posted by Kumar Nirmal Prasad

0/Post a Comment/Comments

Kindly give your valuable feedback to improve this website.

Post a Comment

Kindly give your valuable feedback to improve this website.