[BA 3rd Sem Question Papers, Dibrugarh University, 2012, Mathematics, General, Group A: Coordinate Geometry and Analysis - I (Real Analysis)]
GROUP – A
(Coordinate Geometry)
1. (a) Find where the origin is to be shifted without changing the direction of the axes, so that the terms in x and y are removed from the equation 
Or
If any angular displacement of the coordinate axes transforms the expression 
into the expression
then show that 
into the expressionthen show that 2. (a) Write the condition that the straight lines represented by 
are perpendicular to each other.
are perpendicular to each other. (b) Show that a homogeneous equation of the second degree always represents a pair of straight lines passing through the origin. 3
(c) Find the equations of the pair of straight lines represented by 3
Or
If the pairs of straight lines 
and
be such that each pair bisects the angle between the other pair, then prove that 
andbe such that each pair bisects the angle between the other pair, then prove that (d) If the equation 
represents a pair of straight lines equidistant from the origin, show that 
represents a pair of straight lines equidistant from the origin, show that Or
Show that the area of the triangle formed by the lines represented by and 
is 
and is 3. (a)
(b)
(c)
Or
Find the condition that the lines 
be conjugate diameters of the conic 
be conjugate diameters of the conic SECTION – II
(3-Dimension)
4. (a) Reduce the equation of the plane 
to the normal form.
to the normal form. (b) Write the equation of the plane parallel and at unit distance to 
plane.
plane. (c) Express the equation of the 
in symmetrical form.
in symmetrical form. (d) Find the equation of the plane through the points 
and 
and perpendicular to the plane
. 3
and and perpendicular to the plane. 3Or
Find the equation of the plane passing through the intersection of the planes 
and perpendicular to the plane
.
and perpendicular to the plane. (e) Find the equation of the two planes represented by the equation 3+1=4
Find the angle between them.
Or
Find the coordinates of the foot of the perpendicular drawn from the point 
to the plane 
. Find also the image of the point with respect to the plane.
to the plane . Find also the image of the point with respect to the plane. 5. (a) Find the shortest distance between the lines 3
and
and show that they are coplanar.
Or
A perpendicular is drawn from the origin to the line
Find the equation of the perpendicular and coordinates of its foot.
(b) Find the equation of the line of the shortest distance between the lines 4
and 
Or
Find the surface generated by a straight line which meets the two lines
at the same angle.
at the same angle. GROUP – B
(Analysis – I)
6. (a) Find the 
derivative of 
, where 
and 
.
derivative of , where and . (b) Find the curve whose curvature at any point on it is zero.
(c) Prove that the subnormal at any point of a parabola is of constant length.
(d) Evaluate:
Or
If
, show that
, show that 
7. (a) Verify Roll’s theorem for the function 
in 
2
in 2 (b) Write the remainder after term of Taylor’s series in Lagrange’s Form. 1
term of Taylor’s series in Lagrange’s Form. 1 (c) State and prove Lagrange’s mean value theorem. 4
Or
Using Maclaurin’s theorem, expand sin x in an infinite series in powers of x.
(d) State Darboux’s theorem.
(e) Show that function 
defined by
defined by 
Is continuous at
8. (a) If 
, then show that
, then show that 
(b) If
, prove that
. 2
, prove that. 2Also Read: Dibrugarh University Question Papers
9. (a) Prove that 
, if 3
, if 3
Or
Show that
(b) If
, 
being a positive integer greater than 1, then deduces that
, hence find the value of
.
, being a positive integer greater than 1, then deduces that, hence find the value of.Or
Find the whole length of the curve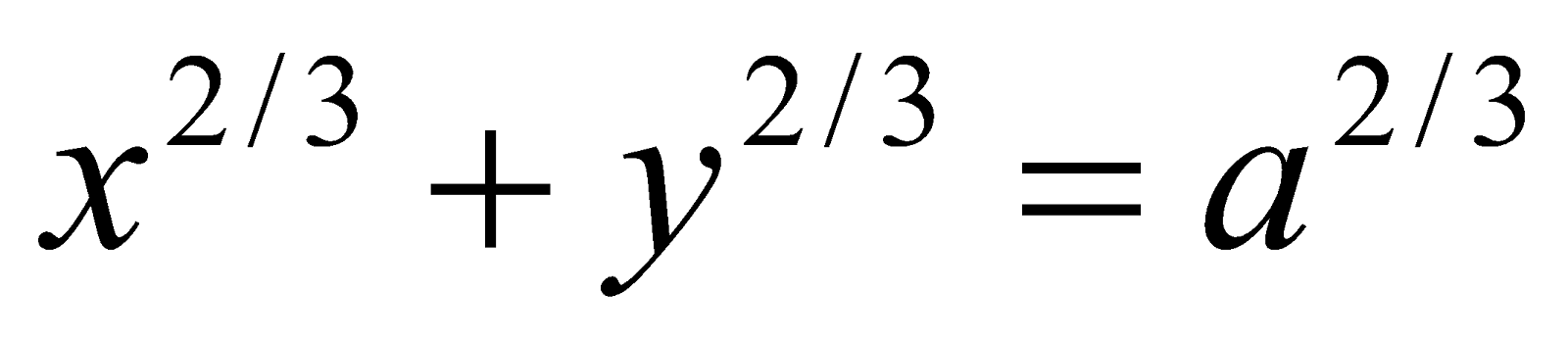
.
. (c) Show that, 
, m, n being positive integers greater than one, then show that 
.
, m, n being positive integers greater than one, then show that .Or
Using reduction formula of
Deduce 
***
Post a Comment
Kindly give your valuable feedback to improve this website.