2013
(November)
MATHEMATICS
(Major)
Course: 504
(Mechanics and Integral Transforms)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
GROUP – A
(Mechanics)
(a): Statics
(Marks: 25)
1. (a) Write the number of ways that a given system of forces acting on a rigid can be replaced by two forces equivalent to the given system. 1
(b) Write the constituent forces of wrench. 1
(c) Write the necessary conditions of equilibrium of a rigid body under the action of a system of forces acting at any point of it. 2
(d) Find the equations of the central axis of a system of forces acting on a rigid body. 6
Or
Find the resultant of any given system of forces acting at given points of a rigid body.
2. (a) Write the virtual work done by tension of an inextensible string. 1
(b) Mention the positions of centre of gravity of a body for stable and unstable equilibrium. 2
(c) Prove that when a rigid body acted upon by a number of coplanar forces by in equilibrium, then the algebraic sum of the virtual work done by the forces in any small displacement, consistent with the geometrical conditions of the system is zero. 7
Or
Derive the Cartesian equation of common catenary.
(d) Find the work done by tension of a light rod. 5
Or
Six equal light rods are joined to form a hexagon ABCEDF, which is suspended at A and F, so that AF is horizontal. A rod BE also light, keeps the figure from collapsing and is of such a length that the rods ending in the points B, E are inclined at angle 450 to vertical. Equal weights W are suspended from B, C, D, E. Find the stress in BE.
(b): Dynamics
(Marks: 25)
3. (a) Write the period of a simple harmonic motion given by the equation 
1
1
(b) Define angular acceleration. 2
(c) Find the resolved parts of acceleration along the tangential and normal directions. 5
Or
The velocity of a particle along and perpendicular to the radius vector are 
and
. Find the equation of the path of the particle.
and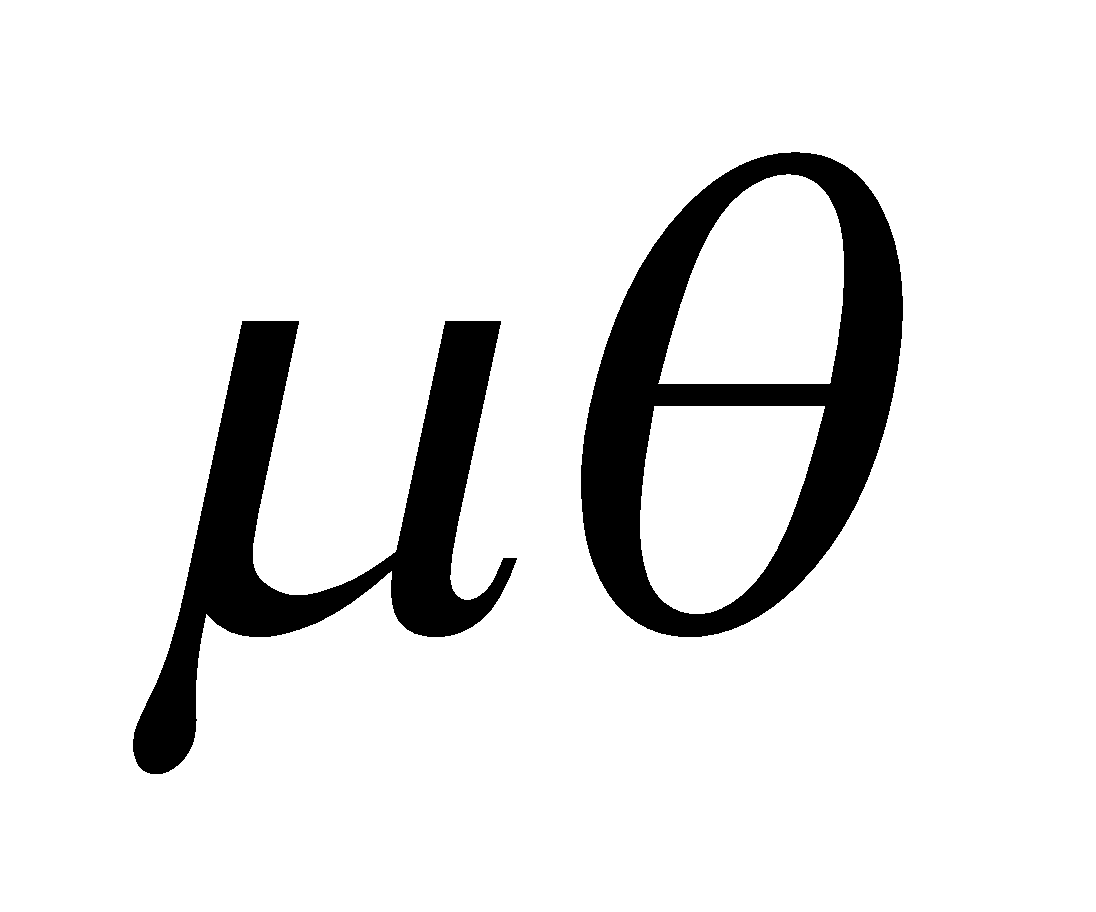. Find the equation of the path of the particle.
4. (a) Write the name of the force which is always directed towards a fixed point. 1
(b) Equation of motion of a falling body is given by
If air resistance 
is considered, then write the corrected equation. 1
is considered, then write the corrected equation. 1
(c) A particle describes the curve 
under a force F to the pole. Find the law of force. 5
under a force F to the pole. Find the law of force. 5
Or
A particle falls under gravity from rest in a medium whose resistance varies as the velocity. Discuss the motion.
5. (a) Write the moment of inertia of a body of elementary mass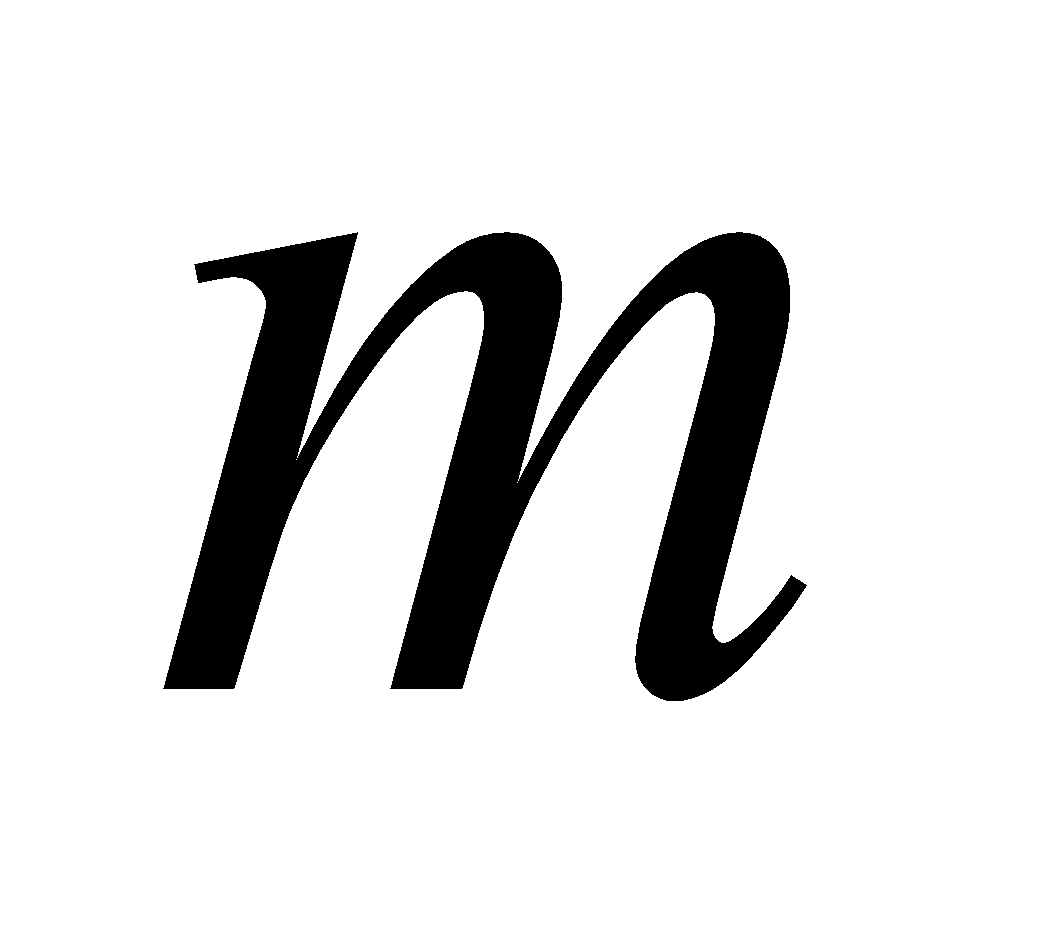 
with respect to pair of axes OY and OZ. 1
with respect to pair of axes OY and OZ. 1
(b) Write the product of inertia of a body of elementary mass 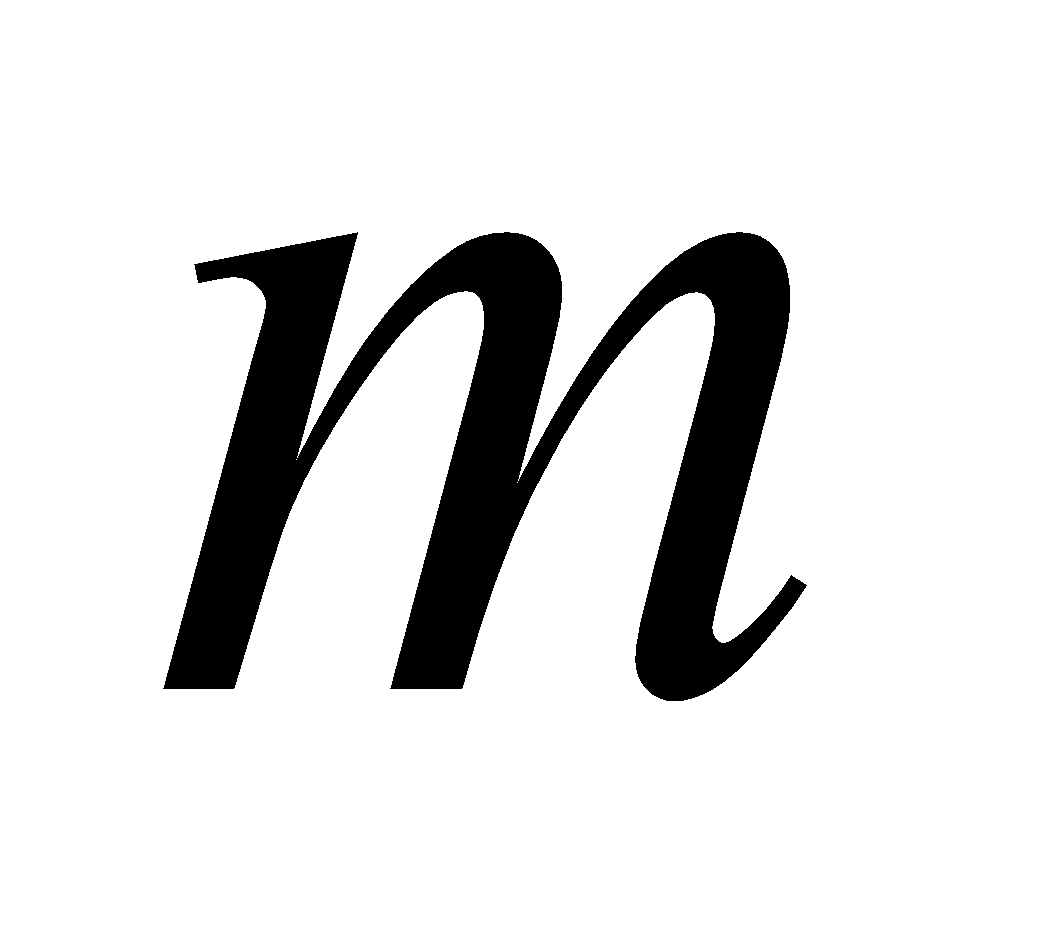with respect to pair of axes OY and OZ. 1
with respect to pair of axes OY and OZ. 1
(c) If 
be the moment of inertia of an element of a uniform rod of length
, then find the moment of inertia of the rod about one end of the rod. 2
be the moment of inertia of an element of a uniform rod of length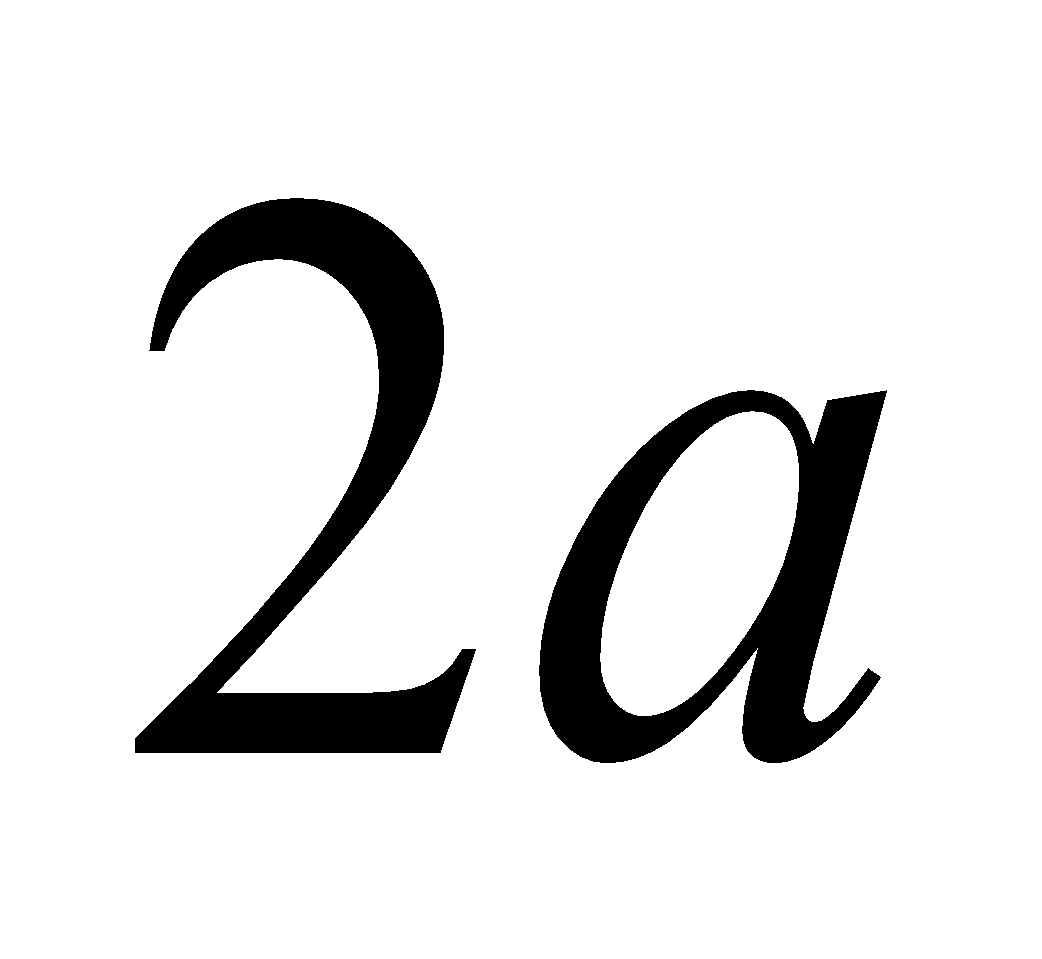, then find the moment of inertia of the rod about one end of the rod. 2
(d) Show that the reversed effective forces acting on each particle of the body and the external forces of the system are in equilibrium. 6
Show that moment of inertia of a body about any axis is equal to its moment of inertia about a parallel axis through its centre of gravity, together with the moment of inertia of the whole mass at its centre of gravity about the axis.
GROUP – B
(Integral Transforms)
(Marks: 30)
6. (a) Write the value of 
. 1
. 1
(b) Find
. 2
. 2
(c) Evaluate
. 2
. 2
(d) Evaluate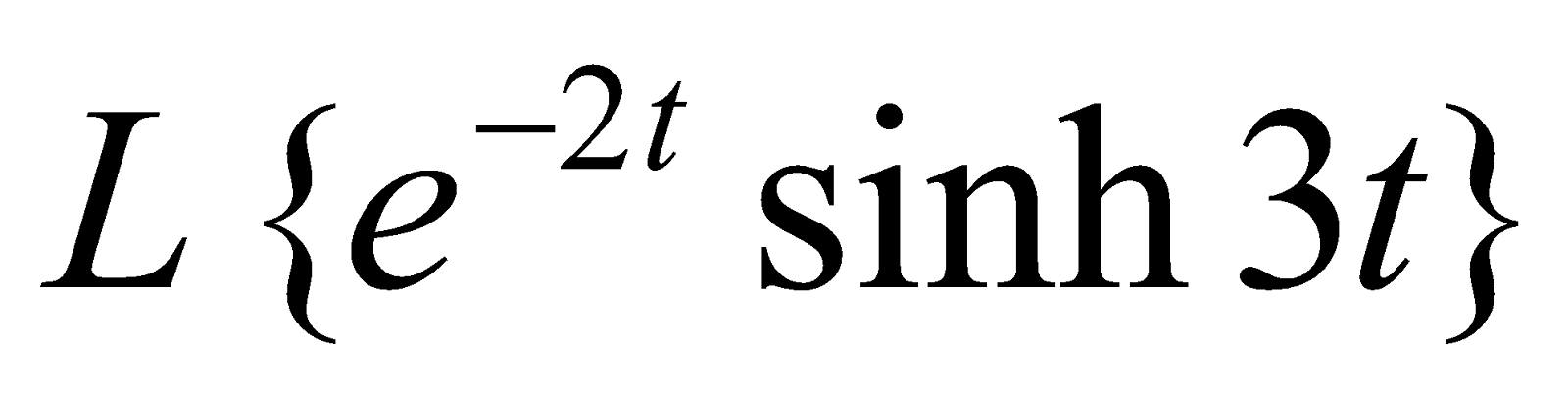
. 3
. 3
Or
Evaluate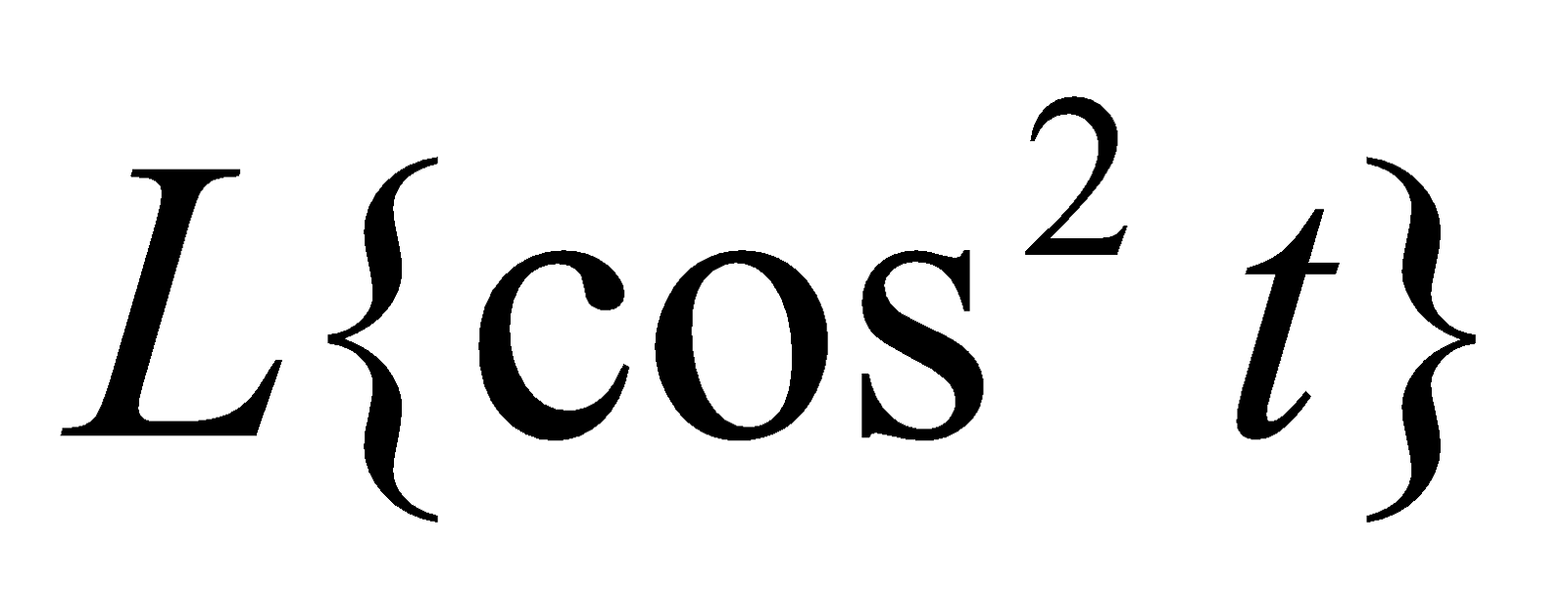
.
.
7. (a) Write the value of 
1
1
(b) Find the value of 
2
2
(c) Evaluate 
5
5
Or
Evaluate 
8. (a) If 
, then write the value of 
. 1
, then write the value of 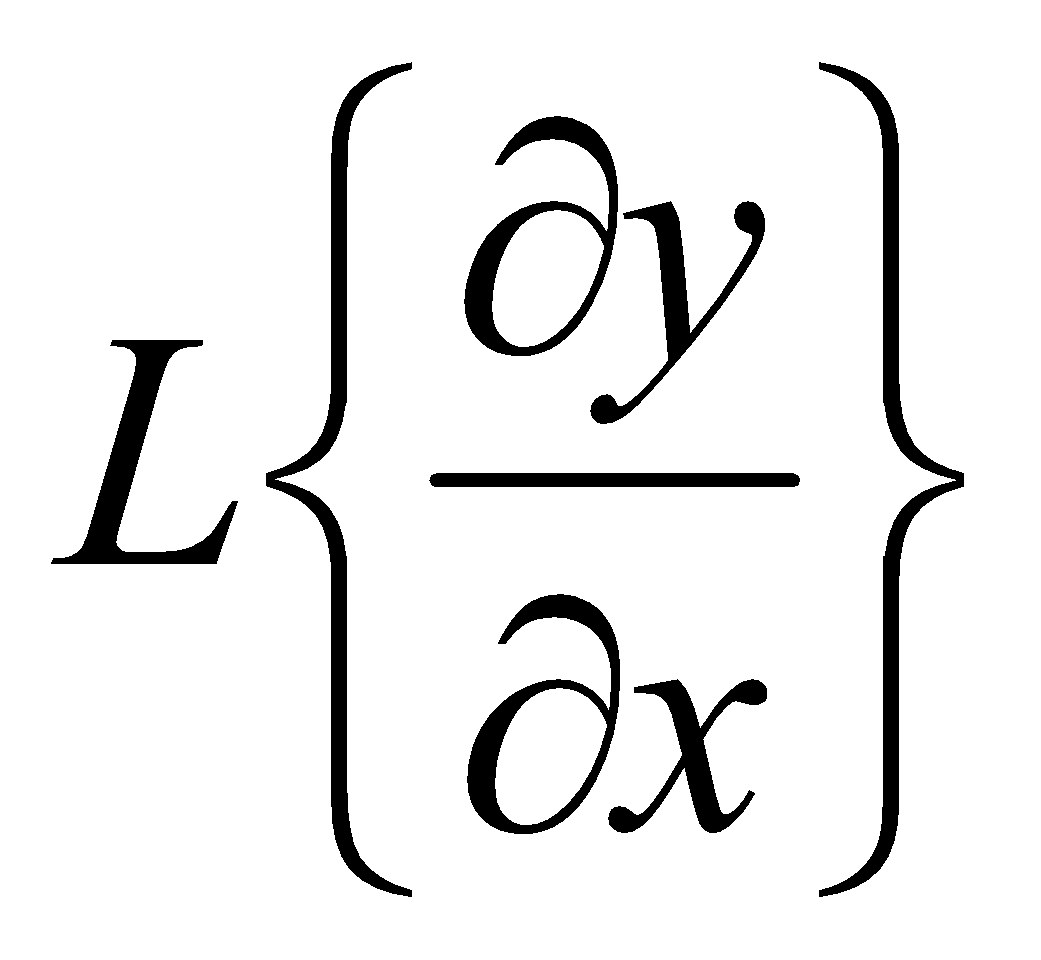. 1
(b) Solve
where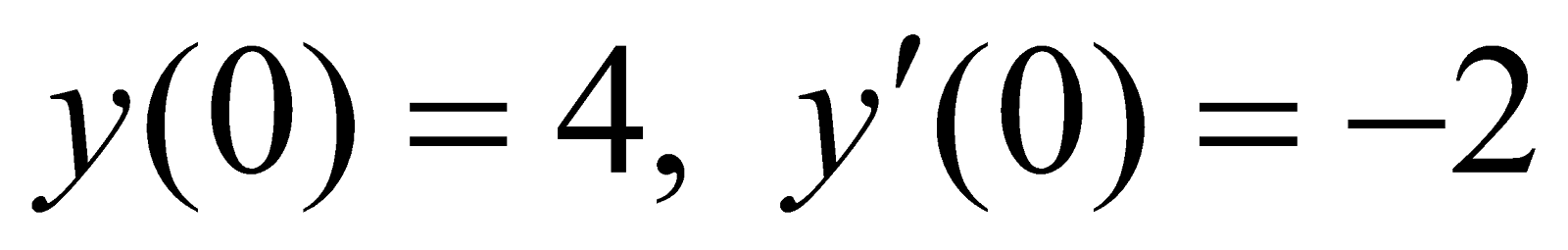 
4
4
(c) Solve
and 
4
4
(d) Solve
where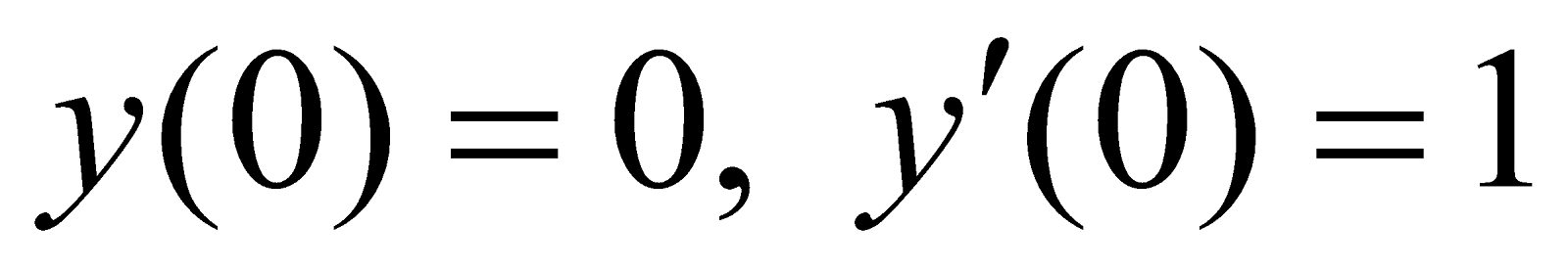 
. 5
. 5
Or
Solve
where 
.
.
***
Post a Comment
Kindly give your valuable feedback to improve this website.