[BA 5th Sem Question Papers, Dibrugarh University, 2013, Mathematics, General, (A) Analysis – II, (B) Mechanics]
(A) Analysis – II (Complex Analysis)
(Marks: 35)
1. (a) Define an analytic function. 1
(b) Show that the function
is harmonic. 3
is harmonic. 3
(c) State and prove the necessary conditions of Cauchy-Riemann equations. 6
Or
Construct the analytic function, when
.
.
2. (a) Define line integral and closed contour. 1+1
(b) Answer any two: 5x2=10
- State and prove Cauchy’s integral formula.
- If
is an analytic function of
and
is continuous at each point within and on a closed contour
, then prove that
- Show that
, if
is analytic in the domain
and its derivative at any point
is again analytic.
3. (a) Write in short (any two): 1+1=2
Isolated singularity, Poles, Removable singularity, Essential singularity
(b) State Taylor’s theorem. Expand
in a Taylor series about
. 2+3=5
in a Taylor series about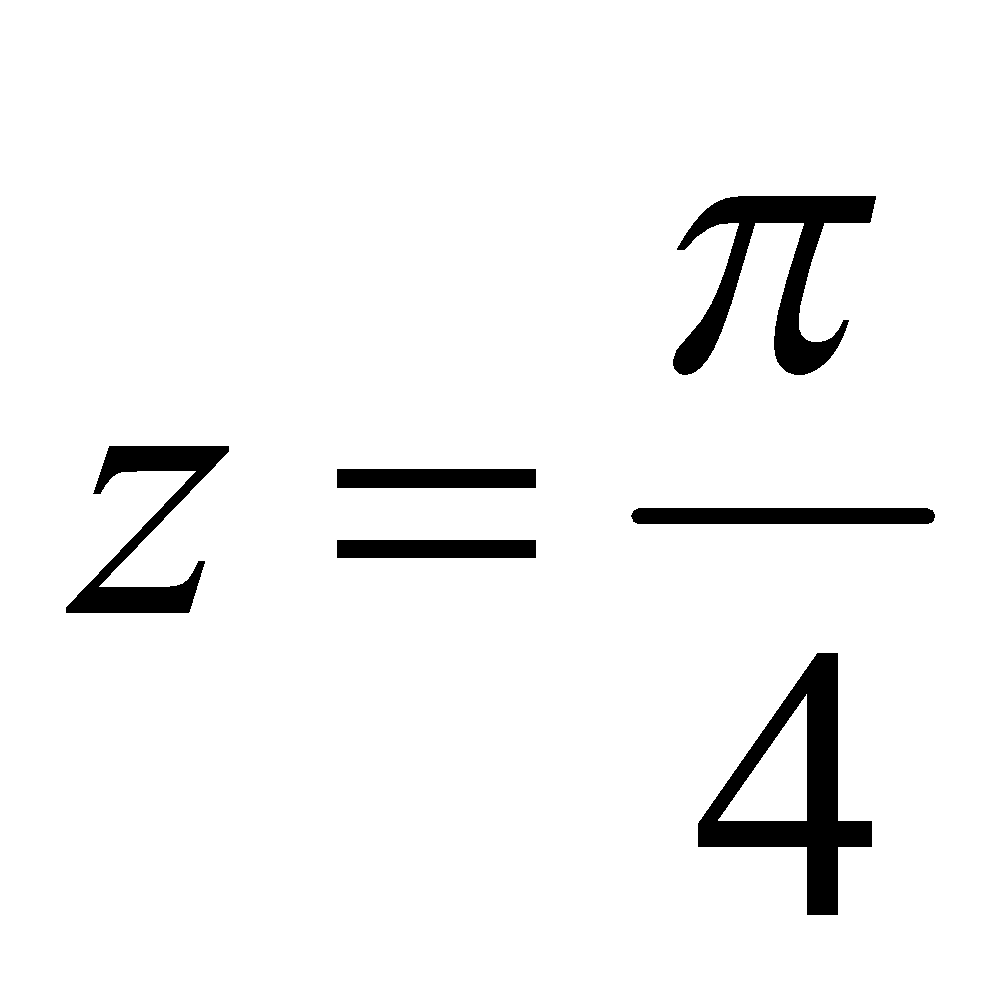. 2+3=5
Or
State Laurent’s theorem and expand 
with the help of this theorem.
with the help of this theorem.
(c) Find the residue of
Or
Find the value of:
, if
(B) Mechanics
(Marks: 45)
(a) Statics
4. (a) What do you mean by screw? 1
(b) Write down the equation of central axis for a finite number of forces acting on a rigid body. 2
(c) Answer any one: 7
- Prove that when a rigid body under the action of the three forces is in equilibrium, the forces are either parallel or concurrent.
- Find the principal pitch of any wrench.
5. Answer any two: 5x2=10
- Explain the forces which can be omitted while forming the equation of virtual work.
- Deduce the Cartesian equation of common catenary.
- A kite flying at a height
withy a length
of wire paid out, and with the vertex of the catenary on the ground, show that at the kite the inclination of the wire to the ground is
, and its tensions there and at the ground are
and
, where
is the weight of the wire per unit length.
(b) Dynamics
6. (a) Define simple harmonic motion and mention its nature. 1+1=2
(b) Answer any one: 6
- The distances of a particle performing SHM from the middle point of its path at three consecutive times observed to be
. Show that the time of the complete oscillation is
- A particle is moving along a curve. Find the acceleration among the tangent and normal to the path of the particle.
7. (a) Find the differential equation of a central orbit in the form 7
(b) A particle under a central acceleration
is projected with velocity
at a distance
, show that the path is a rectangular hyperbola if the angle of projection is
is projected with velocityat a distance, show that the path is a rectangular hyperbola if the angle of projection is 
Also Read: Dibrugarh University Question Papers
8. Answer any two: 5x2=10
- Show that the moment of inertia of a rectangle whose sides are a and b, and mass M about a diagonal is
- Determine the moment of inertia of a thin uniform rod of mass M and length 2a about one end.
- Find the moment of inertia of a thin uniform rod about a line through its centre and perpendicular to its length.
***
Post a Comment
Kindly give your valuable feedback to improve this website.