2014
(May)
MATHEMATICS
(General)
Course: 601
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions.
GROUP – A
[(a) Abstract Algebra
(b) Elementary Statistics]
(a) Abstract Algebra
(Marks: 45)
1. (a) Define binary composition on a set X. 1
(b) What do you mean by cyclic group? 1
(c) If  denotes the cyclic permutation
denotes the cyclic permutation  of a set
of a set  , then what is the length of
, then what is the length of  ? 1
? 1
(d) Is it true that  (alternating group) has no subgroup of order six? 1
(alternating group) has no subgroup of order six? 1
2. If  is a finite non-void subset of a group
is a finite non-void subset of a group , then prove that
, then prove that  is a subgroup of
is a subgroup of  if and only if
if and only if  for all
for all . 4
. 4
3. For each normal subgroup  of a finite group
of a finite group , prove that
, prove that . 2
. 2
Or
If  and
and  are two groups,
are two groups,  and
and their respective identities, and
their respective identities, and  is a homomorphism of
is a homomorphism of  into
into  , then prove that
, then prove that 
4. If ,
,  and
and , then show that
, then show that  and
and  are disjoint permutations. 2
are disjoint permutations. 2
5. State and prove Lagrange theorem for finite group. 1+5=6
6. Prove that a group of order  is cyclic if and only if it has an element of order
is cyclic if and only if it has an element of order  . 5
. 5
Or
What do you mean by a normal subgroup of a group? Prove that subgroup  of a group
of a group  is normal if and only if
is normal if and only if  for every
for every .
.
7. If  is a homomorphism of
is a homomorphism of  onto
onto  and
and  ,
, any normal subgroup of
any normal subgroup of  and
and  then show that
then show that  is normal subgroup of
is normal subgroup of  containing
containing  and
and  . 6
. 6
8. Prove that every group is isomorphic to a permutation group. 6
Or
Prove that the set  of all automorphisms of a group
of all automorphisms of a group  is a group under the resultant composition.
is a group under the resultant composition.
9. Prove that finite non-zero integral domain is a field. 5
Or
If in a ring  with unity,
with unity, 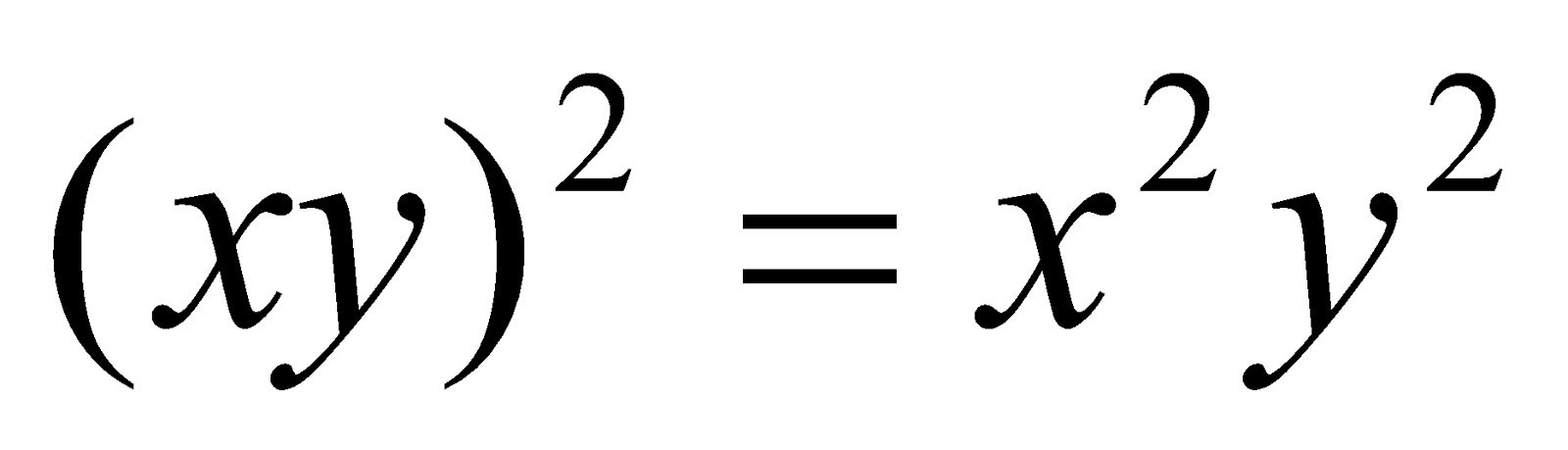 for all
for all  then prove that
then prove that  is commutative.
is commutative.
10. If  is a ring with unity and has no right ideals except
is a ring with unity and has no right ideals except  and
and , then show that
, then show that  is a division ring. 5
is a division ring. 5
(b) Elementary Statistics
(Marks: 35)
11. (a) What is the term used for the total number of possible outcomes of a random experiment? 1
(b) What is the sample space when three coins are tossed? 1
(c) State True or False:  , where
, where  =mean,
=mean,  =SD and
=SD and  =coefficient of variation. 1
=coefficient of variation. 1
(d) What is the shape of normal probability curve with means  . 1
. 1
12. What is the probability that at least two out of people have the same birthday? Assume 365 days in a year and that all days are equally likely. 4
people have the same birthday? Assume 365 days in a year and that all days are equally likely. 4
Or
Three newspapers A, B and C are published in a city. It is estimated from survey that of the adult population: 20% read A, 16% read B, 14% read C, 8% read both A and B, 5% read both A and C, 4% read both B and C, 2% read all three. Find what percentage read at least one of the papers.
13. The first of two samples has 100 items with mean 15 and standard deviation 3. If the whole group has 250 items with mean 15.6 and standard deviation , then find standard deviation of the second group. 4
, then find standard deviation of the second group. 4
14. The chances of solving a mathematical problem correctly by  and
and  are
are  and
and  respectively. If the probability of their making a common errors is
respectively. If the probability of their making a common errors is  and they obtain the same answer, then find the probability that their answer is correct. 5
and they obtain the same answer, then find the probability that their answer is correct. 5
15. Prove that correlation coefficient is independent of the change of origin and scale. 7
Or
Obtain the equations of two lines of regression for the following data. Also obtain the estimate of  for
for  =70:
=70:
X :
|
65
|
66
|
67
|
67
|
68
|
69
|
70
|
72
|
Y :
|
67
|
68
|
65
|
68
|
72
|
72
|
69
|
71
|
16. What do you mean by success and failure in binomial probability distribution?  and
and  play a game in which their chances of winning are in the ratio 3 : 2. Find A’s chance of winning at least three games out of five games played. 1+5=6
play a game in which their chances of winning are in the ratio 3 : 2. Find A’s chance of winning at least three games out of five games played. 1+5=6
Or
GROUP – B
[(a) Discrete Mathematics
(b) Metric Space]
(a) Discrete Mathematics
(Marks: 45)
1. Answer the following questions: 1x5=5
- Determine the truth value of the following statement: “If 3 is even, then 7 is odd.”
- Give one example of chain.
- How many cells are there in a ‘Karnaugh map’ for
variables?
- What is the greatest lower bound of b and d in the lattice given below?
1
d e





a c
0
- State True or False: “q is a valid conclusion of the premise p if and only if p
q is a tautology.”
2. Answer the following questions: 2
- Write the following statement in symbolic form using suitable symbols: “It is raining and very cold today but not a holiday” where p : ‘Today is a holiday’
q : ‘It is raining today’
r : ‘It is very cold today’
- Let
denote
is younger than
. Express
in natural language. 2
- Write the rule of conditional proof. 2
- Write the dual statement of the following:
where a, b, c are in a lattice L. 2
- Write the converse and the contra-positive of the following statement: 3
“If Mr. Lohia is a businessman, then he is rich.”
- Show that the lattice with the following:
‘Hasse diagram’ is complemented but not a distributive lattice: 2+1=3
1 




c
a
b
0
3. Answer any four of the following questions: 4x4=16
- Verify that the proposition
is a tautology.
- Prove that in any lattice
for any
- Draw the Hasse diagram of the lattice
where
the set of all positive divisors of 30 is and
represents the relation of divisibility defined on
.
- For all
,
in a Boolean algebra B, prove that
, where
and
represent complements of
and
respectively in B.
- Obtain the sum-of-products canonical form of Boolean expression of the following:
4. Answer the following questions:
- Check the validity of
from the following premises: 5
- What do you mean by Boolean sub-algebra? If
is a Boolean algebra and
, then show that
is a Boolean sub-algebra of
. 5
(b) Metric Space
(Marks: 35)
5. State either True or False: 1x3=3
- Any non-empty set can be regarded as a metric space by defining suitable metric on it.
- A is open set if and only if A = int (A).
- The real line is not a complete metric space.
6. Prove that 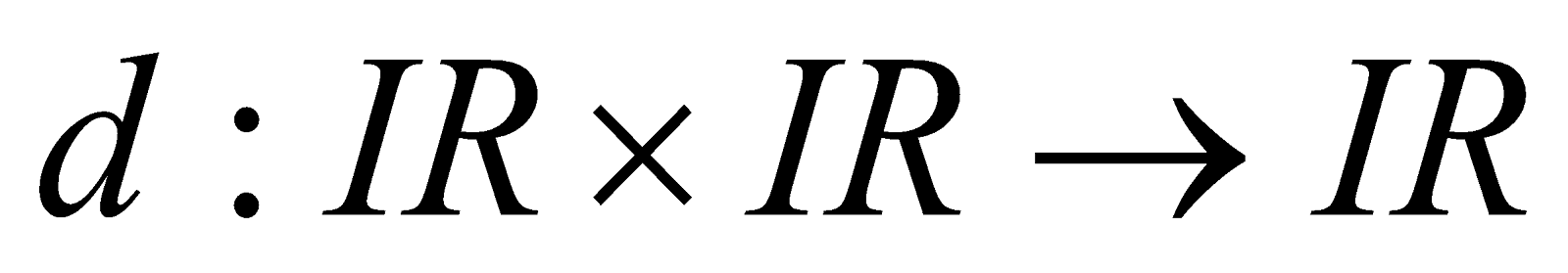 defined by
defined by  is a metric on
is a metric on 4
4
7. Let  be the usual metric on the set of reals
be the usual metric on the set of reals  and
and . Find the distance of
. Find the distance of  from the point 2 and the diameter of
from the point 2 and the diameter of . 1 ½ x2=3
. 1 ½ x2=3
8. Define an open subset of any metric space. Is the subset  an open subset of the metric space
an open subset of the metric space  with usual metric? Give reasons for your answer. Can 1 be a limit point of
with usual metric? Give reasons for your answer. Can 1 be a limit point of  ? 2+1+2+1=6
? 2+1+2+1=6
9. Prove that every convergent sequence  in any metric space is a Cauchy sequence. Is the converse true? 3+1=4.
in any metric space is a Cauchy sequence. Is the converse true? 3+1=4.
10. Let  and
and  be two metric spaces and
be two metric spaces and . When
. When  is said to be – 3
is said to be – 3
- Continuous at a point
- Continuous mapping;
- Uniformly continuous?
Or
Show that the real function  defined on IR by
defined on IR by  is uniformly continuous.
is uniformly continuous.
11. Let  and
and  be metric spaces and
be metric spaces and  be a continuous mapping. Then prove that
be a continuous mapping. Then prove that  is open in
is open in  whenever
whenever  is open in
is open in  . 5
. 5
12. Let , then
, then , the metric space
, the metric space  with usual metric. Find closure of A, interior of A and derived set of A. Verify whether A is a dense subset of
with usual metric. Find closure of A, interior of A and derived set of A. Verify whether A is a dense subset of . 2+2+2+1=7
. 2+2+2+1=7
Or
Define a closed set in a metric space. Prove that in any metric space, a subset is closed  its complement is open. 2+5=7
its complement is open. 2+5=7
***

Post a Comment
Kindly give your valuable feedback to improve this website.