2015
(May)
MATHEMATICS
(Major)
Course: 603
(Algebra II and Partial Differential Equations)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions.
A: Algebra II
(Marks: 40)
1. (a) Choose the correct answer for the following: 1
Isomorphism of a group onto itself is called
- Automorphisms.
- Homomorphism.
- Endomorphism.
- Ideal.
(b) Suppose a group G is an internal direct product of its subgroups H and K, then write the element which is common to both H. and K. 1
(c) Let G be a group and 
and automorphisms of G. If 
, then prove that 
. 3
and automorphisms of G. If , then prove that . 3
(d) Prove that if G is a group, their Aut (G), the set of automorphisms of G is also a group under composition of functions. 4
(e) Let 
,
be normal subgroups of a group
. Then prove that 
is an inner direct product of and if an only if (i) 
and (ii) 
4
,be normal subgroups of a group. Then prove that is an inner direct product of and if an only if (i) and (ii) 4
Or
If 
such that 
is an automorphisms, where 
is some fixed integer, then show that 
for all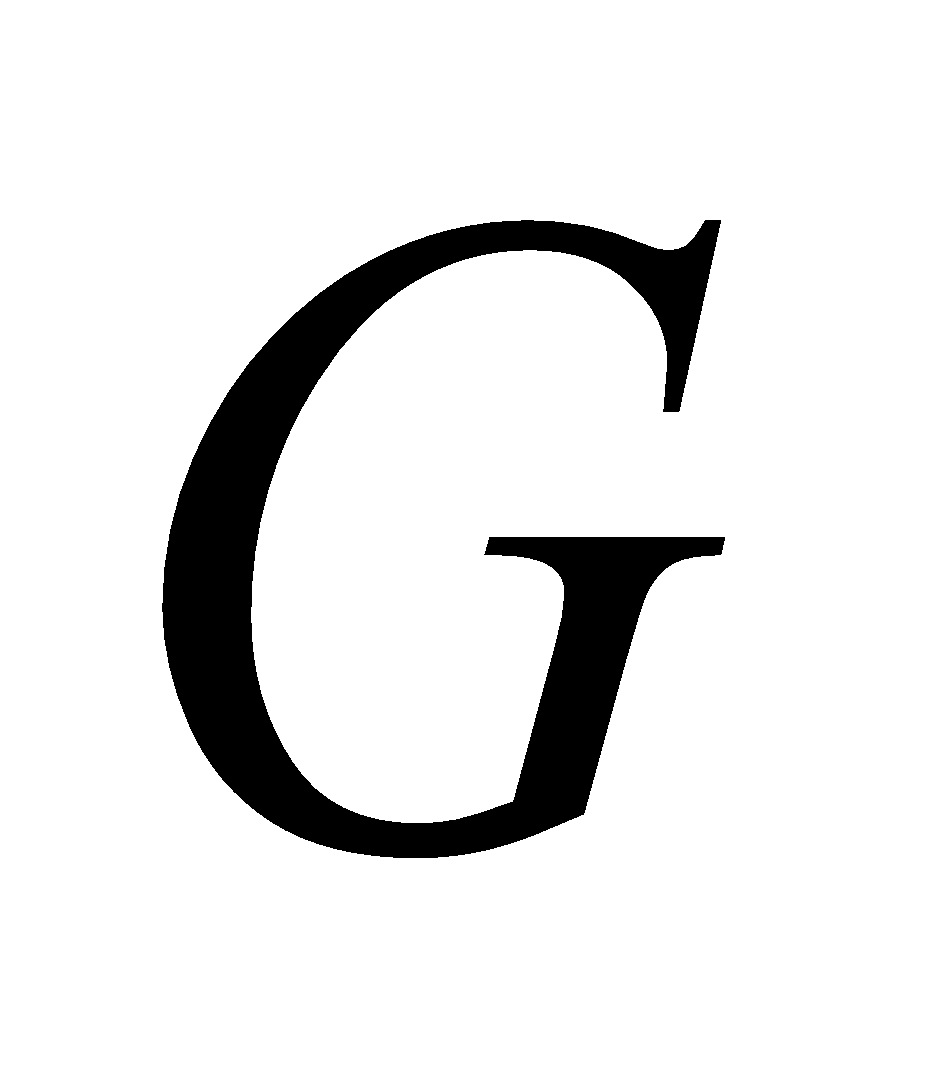
, 
is the centre of group
such that is an automorphisms, where is some fixed integer, then show that for all, is the centre of group
2. (a) Write the binary compositions needed to form a ring in a non-empty set. 1
(b) Write an example of a commutative ring without unity. 1
(c) If R is a ring such that 
then prove that
. 3
then prove that. 3
(d) Show that a Boolean ring is commutative. 4
(e) Prove that a commutative ring R is an integral domain if and only if for all 4
Or
Show that intersection of any two left ideals of a ring is again a left ideal of the ring.
3. (a) Write the another name of the ring of all equivalent classes. 1
(b) Let 
be an onto homomorphism, where 
is a ring with unity. Show that 
is unity of 
3
be an onto homomorphism, where is a ring with unity. Show that is unity of 3
(c) If be an onto homomorphism, then prove that is isomorphic to a quotient ring of . 5
be an onto homomorphism, then prove that is isomorphic to a quotient ring of . 5
Or
Prove that any ring can be imbedded into a ring with unity.
(d) Let 
be a commutative ring with unity. Prove that an ideal 
of 
is maximal ideal of 
if 
is a field. 5
be a commutative ring with unity. Prove that an ideal of is maximal ideal of if is a field. 5
Or
Show that in a Boolean ring, every prime ideal 
is maximal.
, every prime ideal is maximal.
B: Partial Differential Equations
(Marks: 40)
4. (a) Write the number of arbitrary constants that the solution of the partial differential equation 
, where 
possesses. 1
, where possesses. 1
(b) Write the auxiliary equations of the equation
. 1
. 1
(c) Solve any two equations: 4x2=8
(d) Solve any one equation: 5
(e) Find the integral surface of the linear partial differential equation. 5
which contains the straight line? 
5. (a) In Charpit’s method for solving a partial differential equation, a second equation is introduced. Write the order of the equation. 1
(b) Write the complete integral of the equation 
1
1
(c) Write the Charpit’s auxiliary equations for the equation
. 2
. 2
(d) Find complete integrals of any three of the following: 4x3=12
(e) Find a complete integral of 
using Jacobi’s method. 4
using Jacobi’s method. 4
***
Post a Comment
Kindly give your valuable feedback to improve this website.