2015
(November)
MATHEMATICS
(Major)
Course: 502
(Linear Algebra and Number Theory)
Full Marks: 80
Pass Marks: 32
Time: 3 hours
The figures in the margin indicate full marks for the questions
GROUP - A
(Linear Algebra)
(Marks: 40)
1. (a) Write when a system of linear equations is said to be consistent. 1
(b) Show that the additive inverse of any vector in a vector space is unique. 2
(c) Find the solution set for the following system of equations: 3
And 
2. Answer any two of the following:
- Let
and
be two subspaces of a vector space
over a field
. Show that
is also a subspace of
. 4
- When is a set
of vectors in a vector space
said to be linearly independent? Examine whether the vectors
and
of
are linearly independent over
, where
are non-zero real numbers. 1+3=4
- Show that the vectors
,
and
from a basis for
4
3. Define subspace of a vector space with an example. If 
is a proper subspace of a finite dimensional vector space
, then prove that is finite dimensional and
. 2+3=5
is a proper subspace of a finite dimensional vector space, then prove that is finite dimensional and. 2+3=5
4. Answer any three of the following:
- Define a line in a vector space. Prove that any two distinct points determine a unique line in any vector space. 1+2=3
- Let
and
be a fixed vector in
is an affine space of
- Let
. Show that two cosets
and
are equal if and only if
where
. 3
- Let
spanned by
and
. Find the basis for the quotient space
. 3
5. Answer any two of the following:
- Let
be the mapping defined by
Prove that 
is a linear mapping. Also find the basis and the dimension of the image of
is a linear mapping. Also find the basis and the dimension of the image of
2+3+1=6
- Define a linear operator on a vector space with an example. Let
be a linear operator on
given by
. Find the matrix of
where
and
. 2+4=6
- Define isomorphism of vector spaces. Prove that the mapping
from 
to 
is an isomorphism. 2+4=6
to is an isomorphism. 2+4=6
GROUP – B
(Number Theory)
(Marks: 40)
6. (a) If 
and 
are relatively prime, then prove that 
and 
. 2
and are relatively prime, then prove that and . 2
(b) Find the integers 
and 
such that
. 2
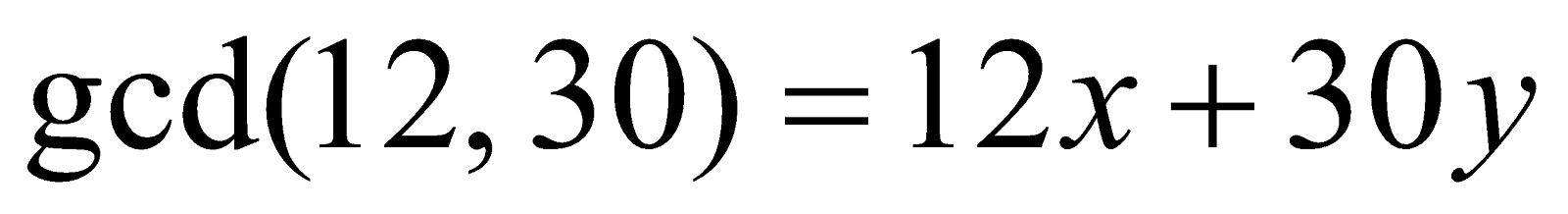and such that. 2
(c) Use division algorithm to establish that the cube of any integer has one of the forms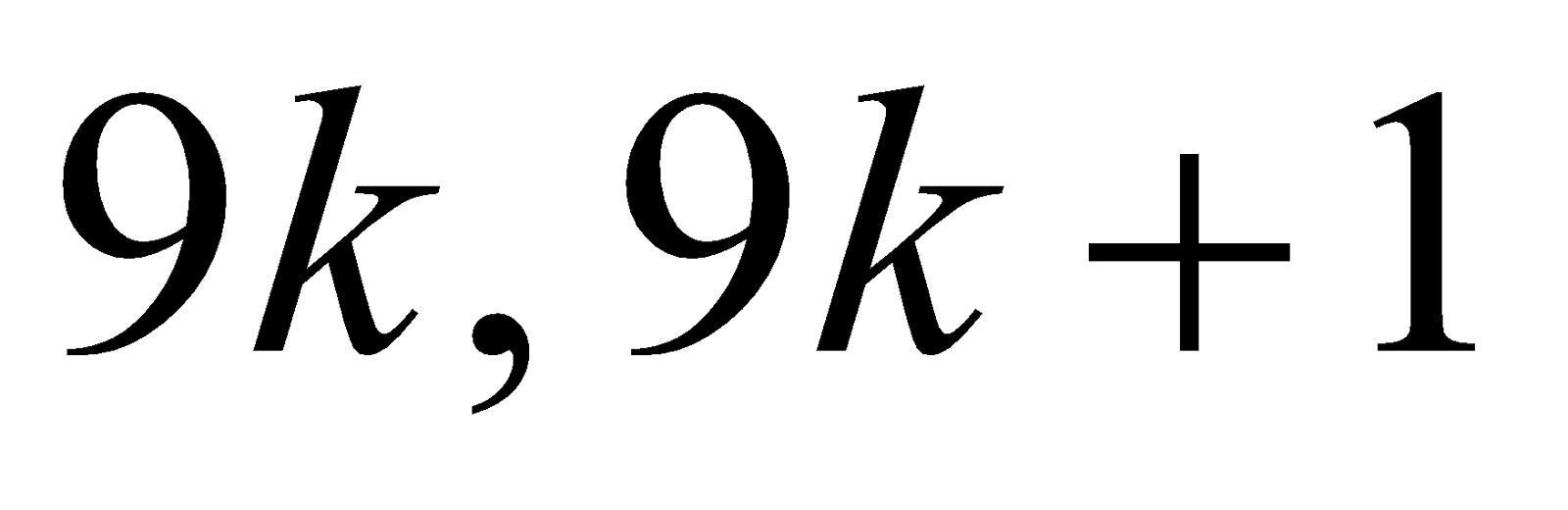 
or
. 3
or. 3
7. (a) Find the number of divisors of 3 and 5 in between 500 and 1000. 3
(b) Find the highest power of 5 which is contained in 200!. 2
(c) If 
and 
are two integers such that
, then show that 
or 
. 3
and are two integers such that, then show that or . 3
8. (a) Write a reduced set of residues modulo 9. 1
(b) Find the remainder when the following sum is divided by 15: 3
(c) Write the condition that is to be satisfied so that 
gives 
. 1
gives . 1
(d) Find the remainder when 
is divided by 7. 2
is divided by 7. 2
(e) Does there exist any solution for the linear congruence 
If so, find all of them. 1+4=5
If so, find all of them. 1+4=5
(f) Solve: 
3
3
9. (a) If 
and 
are positive integers with 
, then prove that 2
and are positive integers with , then prove that 2
(b) Find the value
. 2
. 2
(c) Show that if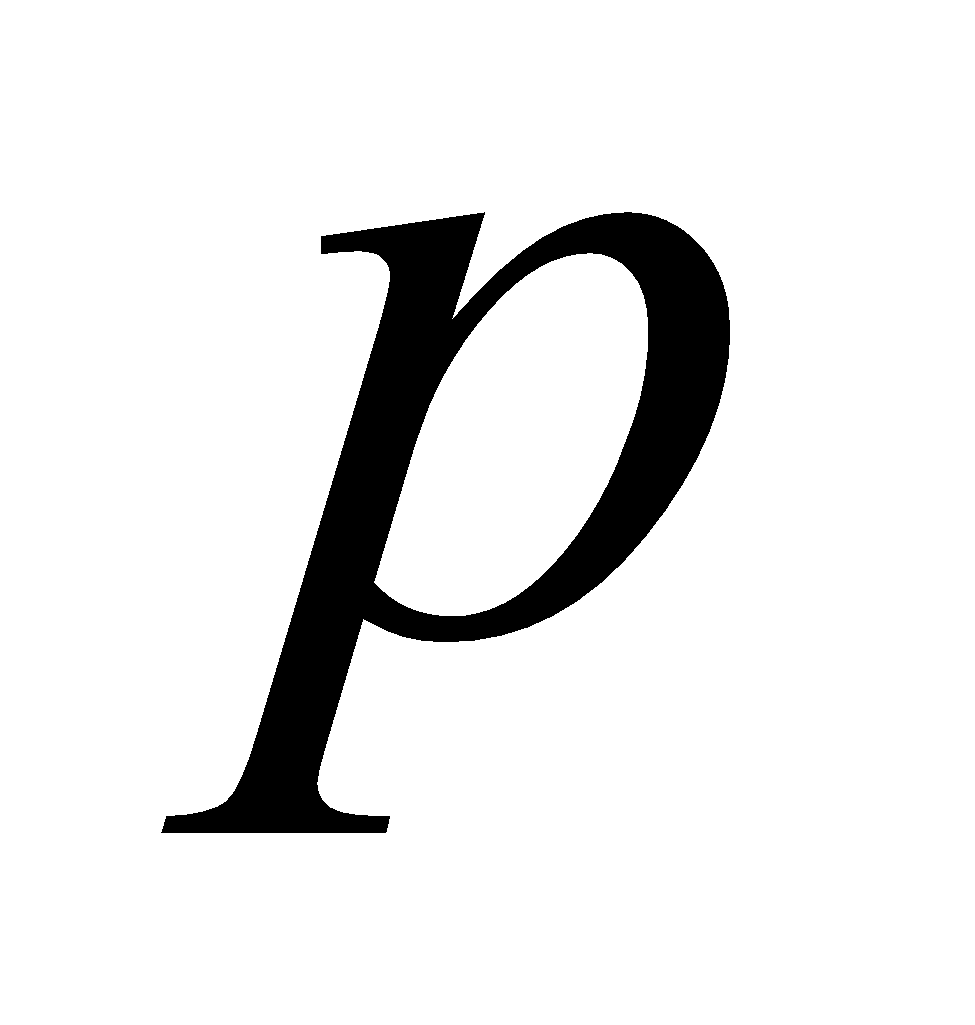
is a prime number, then
is a prime number, then
2
(d) Define a multiplicative arithmetic function. Prove that the Mobius 
-function is multiplicative function. 1+3=4
-function is multiplicative function. 1+3=4
Or
Prove that there are infinitely many primes. 4
***
Post a Comment
Kindly give your valuable feedback to improve this website.