[BA 5th Sem Question Papers, Dibrugarh University, 2013, Mathematics, Major, Logic and Combinatorics, and Analysis - III]
(A) Logic and Combinatorics
(Marks: 35)
1. (a) Define truth function. 1
(b) Let
be ‘it is cold’ and
be ‘it is raining’. Give verbal sentence which describes each of the following: 2
be ‘it is cold’ andbe ‘it is raining’. Give verbal sentence which describes each of the following: 2
(c) Construct the truth table for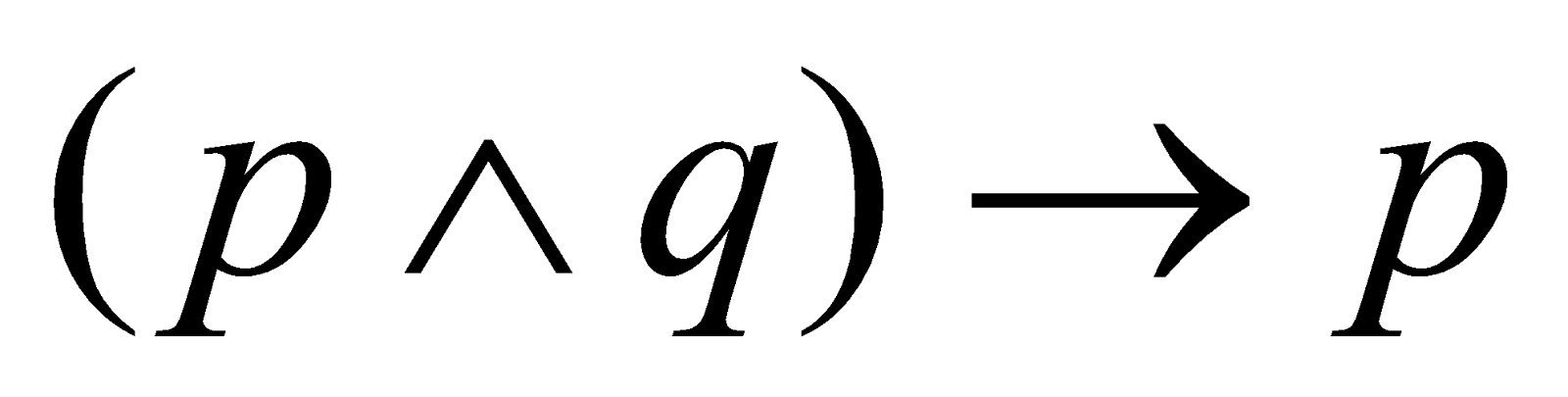
. State whether it is a tautology or not. 3
. State whether it is a tautology or not. 3
(d) Prove that every truth function can be generated by
. Can you generate a truth function by using 
and 
only? 4
. Can you generate a truth function by using and only? 4
Or
Give the arithmetic representation of the form
. Also show that 
. Also show that
2. (a) What do you mean by equivalent statements? 1
(b) Write the rule p and rule t. 2
(c) Translate into symbols 3
- Not all birds can fly.
- Anyone can do it.
- Some people are intelligent.
(d) Derive any one of the following: 4
- Everyone who buys a ticket receives a prize. Therefore, if there is no prize, there nobody buys ticket.
- All men are mortal. Ram is a man. Hence Ram is mortal.
3. (a) State the Pascal’s identity. 1
(b) Find the coefficient of 
in
. 2
in. 2
(c) Define Ramsey number
. Prove that
. 4
. Prove that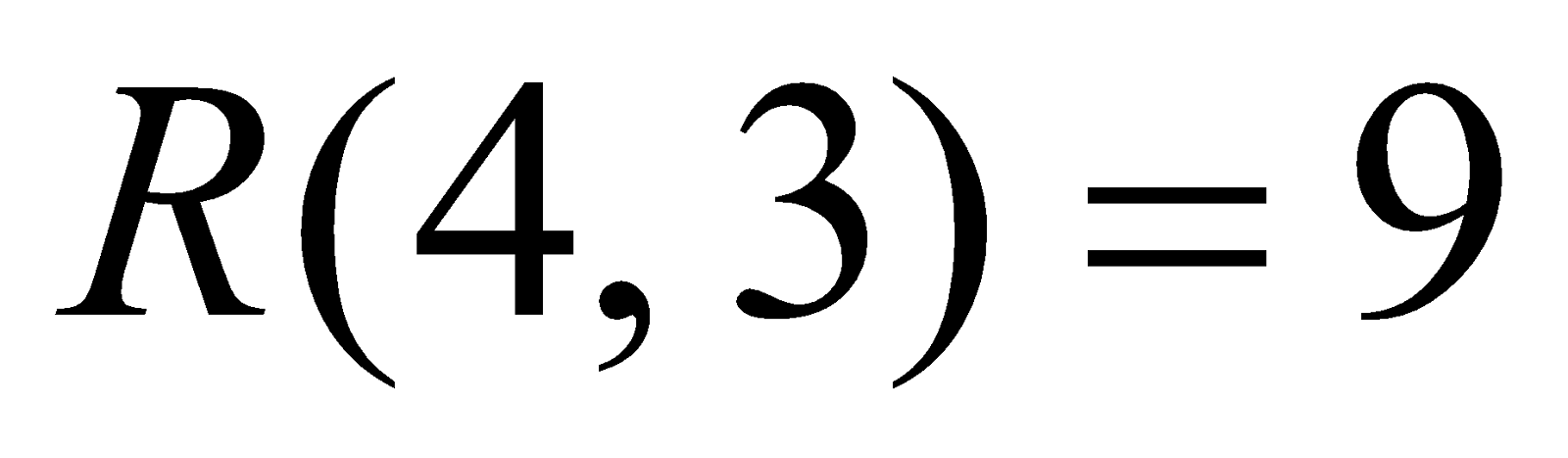. 4
Or
Define Catalan numbers. Prove that 
Catalan number
Catalan number
4. (a) State the pigeonhole principle. 1
(b) How many integers between 100 and 700 are divisible by 3 or 5? 3
(c) Prove that given any 12 natural numbers we can choose 2 of them such that their difference is divisible by 11. 4
Or
Define binomial generating function. Find both binomial and exponential generating functions for the sequence 2, 2, 2, 2, ....
(B) Analysis – III (Complex Analysis)
(Marks: 45)
5. (a) State the condition under which a function is said to be analytic. 1
(b) Define harmonic function. Show that 
is harmonic. 3
is harmonic. 3
(c) State and prove the necessary conditions for a function
to be analytic at all points in a region
. 6
to be analytic at all points in a region. 6
Or
Show that
is not analytic at the origin, although Cauchy-Riemann equations are satisfied. What is your opinion in this case?
6. (a) Define Jordan’s arc.
(b) Find the value of the integral
where 
.
.
(c) State and prove Cauchy’s integral theorem.
(d) If a function 
is analytic for all finite values of 
and is bounded, then show that it is constant. 6
is analytic for all finite values of and is bounded, then show that it is constant. 6
Or
Evaluate:
, where
is
, where
is
7. (a) State and prove Taylor’s series. 1+5=6
(b) Expand 
is Laurent’s series, where
. 2
is Laurent’s series, where. 2
8. (a) Define an isolated singular point of a function 
. 1
. 1
(b) Discuss the singularity of
at 
2
2Also Read: Dibrugarh University Question Papers
(c) Evaluate (any two): 5x2=10
, where
is
***
Post a Comment
Kindly give your valuable feedback to improve this website.